Circle 2C
Overview
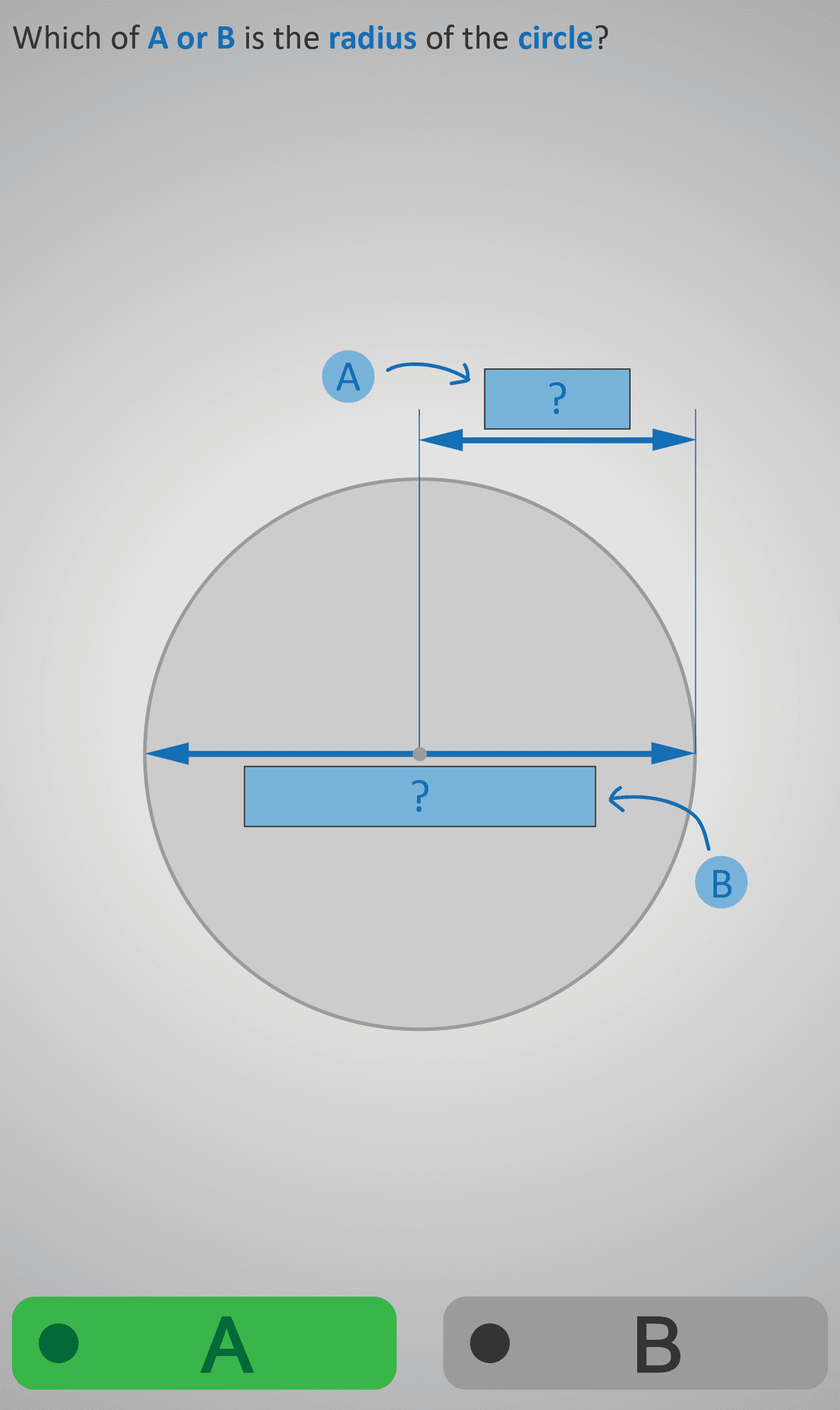
This activity helps students identify and calculate the radius of a circle. In the first screen, learners choose between two line segments, A or B, to decide which one represents the radius. Line A correctly shows the radius, as it goes from the centre of the circle to its edge.
In the second screen, the diameter is given as 22 cm. Students calculate the radius by dividing the diameter by 2, giving 11 cm.
In the third screen, the diameter is 16 m. Again, halving the diameter gives a radius of 8 m.
Through these steps, students reinforce the concept that Radius = Diameter ÷ 2. This sequence builds understanding of the relationship between radius and diameter, and helps learners switch confidently between the two.
Prerequisite Knowledge Required
- Circle 2A – understanding the difference between radius and diameter.
- Measure 1 – familiarity with basic metric units (cm, m).
- Multiply & Divide 1 – confidence in halving and doubling numbers.
Main Category
Geometry – Circles and Measurement
Estimated Completion Time
Approx 6–8 seconds per question. 10 questions total. Total time: ~1–1.5 minutes.
Cognitive Load / Step Size
Low — each step introduces a single, clear concept: identify the radius → calculate radius from diameter → repeat with different units. Well-sequenced for consolidation rather than discovery.
Language & Literacy Demand
Low — concise instructions with supportive visuals. Mathematical notation (÷2) is used clearly and consistently, requiring minimal reading comprehension.
Clarity & Design
Excellent — diagrams use clean, labelled circles with centre points and line segments marked distinctly. The consistent visual style reinforces conceptual clarity rather than decoration.
Curriculum Alignment
Aligned with Geometry and Trigonometry – Circles in the Irish Junior Cycle Mathematics Curriculum:
- Recognise and use the relationship between radius, diameter, and circumference.
- Perform calculations involving measurement of geometric figures.
Engagement & Motivation
Moderate to high — the visual tasks and immediate feedback keep learners engaged. The simplicity of the progression supports a sense of success and confidence-building.
Error Opportunities & Misconceptions
- Confusing the diameter with the radius.
- Forgetting to halve when moving from diameter to radius.
- Misreading metric units (e.g., cm vs m).
Transferability / Real-World Anchoring
High — applicable to geometry, construction, design, and real-world circular measurements (e.g., wheels, lids, clocks).
Conceptual vs Procedural Balance
Balanced — combines conceptual understanding of the radius–diameter relationship with procedural fluency in simple division.
Learning Objectives Addressed
- Identify the radius of a circle on a diagram.
- Calculate the radius when the diameter is given.
- Apply the relationship radius = ½ × diameter using correct units.
- Develop familiarity with metric measurement in geometric contexts.
What Your Score Says About You
- Less than 5: You may be confusing radius and diameter — revisit how they relate.
- Between 6–7: You understand the concept but need to check calculations more carefully.
- Between 8–9: You show strong understanding and accuracy in finding the radius.
- 10/10: Excellent mastery — you can confidently identify and calculate the radius in any context.