Pythagoras 2
Overview
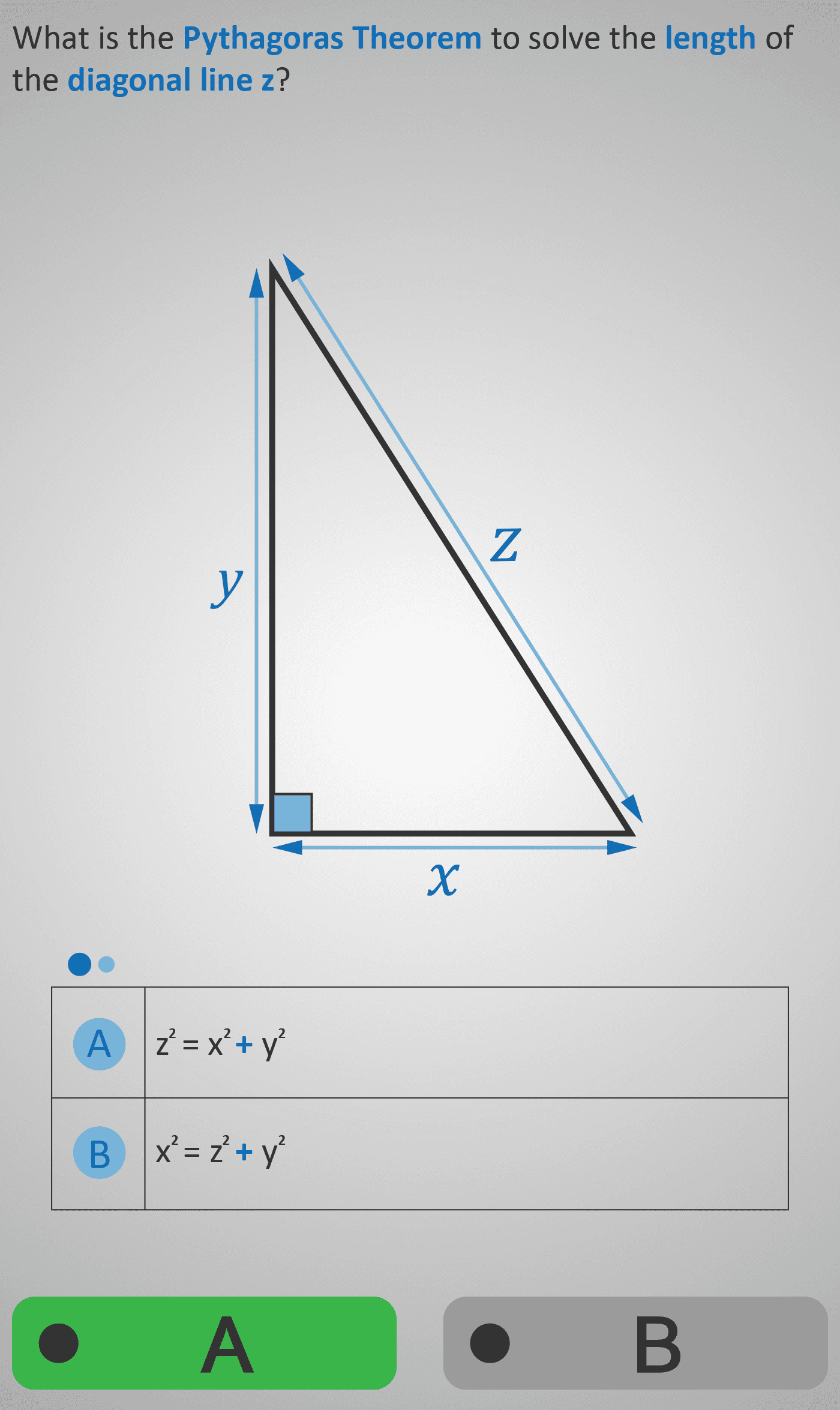
This set builds on the basics of Pythagoras’ Theorem, moving from the general rule to applying it in worked examples with numbers. Students first identify the correct form of the theorem for a right-angled triangle, recognising that the square of the hypotenuse equals the sum of the squares of the other two sides. They then substitute actual side lengths into the theorem, deciding which equation is set up correctly.
The progression continues with different triangle orientations and variable labels, ensuring learners can generalise the rule beyond a single diagram. Finally, students practise applying the theorem with specific measurements, reinforcing the correct structure of the equation and preparing to solve for unknown lengths in later levels.
This sequence helps learners:
- Recognise the hypotenuse as the longest side opposite the right angle.
- Recall and write Pythagoras’ Theorem correctly.
- Substitute given values into the theorem.
- Identify which equation is set up correctly when side lengths are known.
The tasks are scaffolded to move from recognising the rule, to applying it with symbols, and then to applying it with numbers — building confidence before moving on to calculating unknowns.
Prerequisite Knowledge Required
- Understanding of right-angled triangles and basic side labelling (from Hyp–Adj–Opp 2).
- Familiarity with squaring numbers (× itself).
- Basic algebraic substitution skills (from Algebra 2B or 2E).
Main Category
Geometry / Algebra
Estimated Completion Time
Approx 6-10 seconds per question. 20 questions total. Total time: 2-4 minute.
Cognitive Load / Step Size
Moderate — students transition from conceptual recognition to symbolic substitution. The scaffolded structure (rule → substitution → verification) ensures steady cognitive progression without overload.
Language & Literacy Demand
Medium — includes symbolic notation (a² + b² = c²) and some mathematical vocabulary (hypotenuse, opposite). Step-by-step phrasing supports comprehension.
Clarity & Design
Strong — clear right-angle markers, side labels, and colour-coded triangles guide attention. Diagrams are consistent but rotated to test generalisation, reinforcing understanding rather than memorisation.
Curriculum Alignment
Irish Junior Cycle Mathematics – Geometry & Trigonometry Strand:
- “Apply Pythagoras’ Theorem to solve problems in right-angled triangles.”
- “Recognise the relationship between sides of right-angled triangles.”
Engagement & Motivation
Moderate to High — visual diagrams and substitution steps create a sense of discovery. Each example feels like solving a small puzzle, maintaining curiosity through variety.
Error Opportunities & Misconceptions
- Common errors include identifying the wrong side as the hypotenuse or misplacing values in the formula.
- Visual emphasis and structured question flow address these directly.
Transferability / Real-World Anchoring
Moderate — prepares students for later applications in measurement, navigation, and construction problems involving right angles.
Conceptual vs Procedural Balance
Balanced — combines conceptual understanding of the theorem with procedural accuracy in substitution and setup.
Learning Objectives Addressed
- Identify and label sides of a right-angled triangle correctly.
- Recall and write Pythagoras’ Theorem (a² + b² = c²).
- Substitute given side lengths into the theorem correctly.
- Verify which equation correctly represents a given triangle.
What Your Score Says About You
- Less than 5: Needs more practice identifying triangle sides and setting up the theorem.
- 6–7: Understands the rule but may confuse side labels or substitution order.
- 8–9: Good conceptual understanding and accurate application.
- 10 / 10: Excellent — confidently applies Pythagoras’ Theorem to multiple contexts and orientations.