Reciprocal 2
Overview
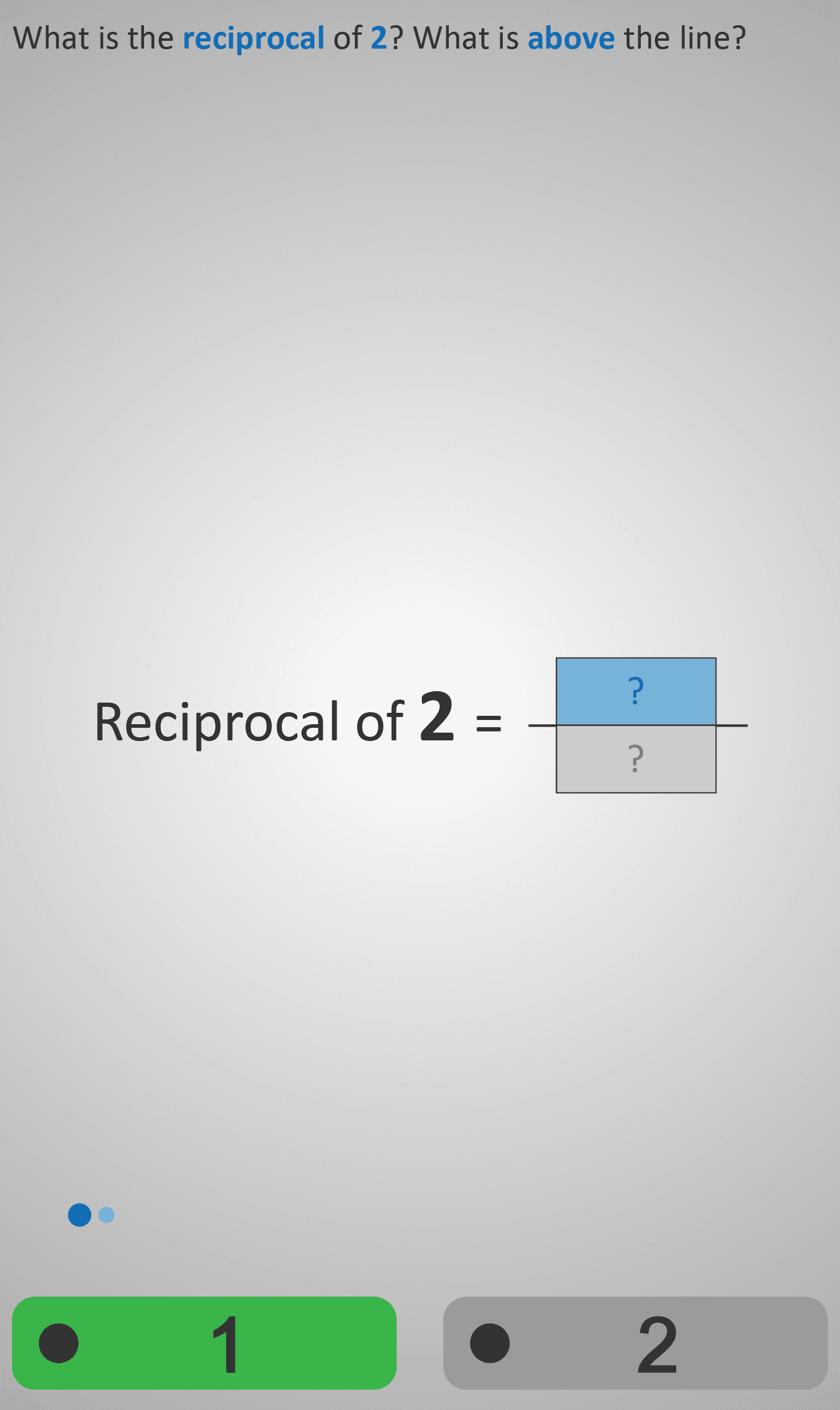
Introduces learners to the concept of reciprocals in fractions by focusing on the numerator (top number) and denominator (bottom number). The lesson begins with the reciprocal of 2, guiding students to identify what goes above the line (numerator = 1) and what goes below the line (denominator = 2), building the fraction 1/2.
It then extends the same reasoning to the reciprocal of 3, reinforcing the pattern that the reciprocal of a whole number is always 1 divided by that number. Learners are asked to select the correct values for both numerator and denominator in multiple-choice steps, with visual fraction boxes showing the “above” and “below” positions.
By the end, students will clearly see that:
Reciprocal of 2 = 1/2
Reciprocal of 3 = 1/3
This step-by-step approach strengthens fraction foundations and prepares learners to apply reciprocals in later topics like division of fractions and algebra.
Prerequisite Knowledge Required
- Linked Phlows: Fraction 2B – finding equivalent fractions and understanding numerator/denominator positions.
- Division 2 – interpreting division as “how many times does one number fit into another.”
- Numbers 2A – comparing greater and smaller values to understand “1 divided by a number.”
Main Category
Fractions & Ratios
Estimated Completion Time
Approx 6–10 seconds per question. 20 questions total. Total time: 2–4 minutes.
Cognitive Load / Step Size
Low — each step isolates one new element: first introducing the concept of “1 over a number,” then generalising from 2 to 3. Transitions are gentle, ensuring learners consolidate the structure of a reciprocal without introducing complex notation or operations.
Language & Literacy Demand
Low — instructions are concise, focusing on key mathematical terms (“numerator,” “denominator,” “reciprocal”). The use of fraction boxes with “above” and “below” labels reduces dependence on reading comprehension, making the visual representation self-explanatory.
Clarity & Design
Highly clear — visual fraction models clearly show which number goes where. The interactive multiple-choice format highlights “top” vs “bottom,” directly supporting understanding of fraction construction rather than relying on memorisation.
Curriculum Alignment
Irish Curriculum Strand: Number
- Recognise and represent fractions as part–whole relationships.
- Understand reciprocals as multiplicative inverses of whole numbers.
- Use fractions to express division of 1 by a whole number.
Engagement & Motivation
Moderate — the interactive layout (filling numerator and denominator positions) provides a tactile sense of building a fraction. While abstract in concept, the visual stepwise design maintains engagement through clarity and immediate feedback.
Error Opportunities & Misconceptions
- Reversing numerator and denominator (e.g., thinking the reciprocal of 2 is 2/1).
- Believing that reciprocals only apply to fractions, not whole numbers.
- Forgetting that the numerator must always be 1 when finding reciprocals of whole numbers.
Each question isolates one potential misconception, helping learners correct errors through comparison and repetition.
Transferability / Real-World Anchoring
Moderate — while abstract, reciprocals underpin many real-world applications like rates, ratios, and inverse relationships (e.g., “1 divided by time = speed”). Builds a bridge toward proportional reasoning and algebraic manipulation.
Conceptual vs Procedural Balance
Conceptual-heavy — focuses primarily on understanding why the reciprocal is 1 divided by the number, before procedural fluency is introduced in higher levels. Builds deep foundational understanding rather than rote memorisation.
Learning Objectives Addressed
- Define and identify the reciprocal of a whole number.
- Recognise the structure of fractions (numerator/denominator).
- Understand reciprocal as an inverse relationship.
- Prepare for later use of reciprocals in fraction division and algebraic expressions.
What Your Score Says About You
- Less than 5: Needs more practice distinguishing numerator and denominator roles.
- 6–7: Understands the pattern but occasionally reverses the fraction.
- 8–9: Strong grasp of reciprocals and fraction structure.
- 10 / 10: Excellent mastery — clearly understands both the concept and representation of reciprocals.