Sin Cos Tan 2

Overview

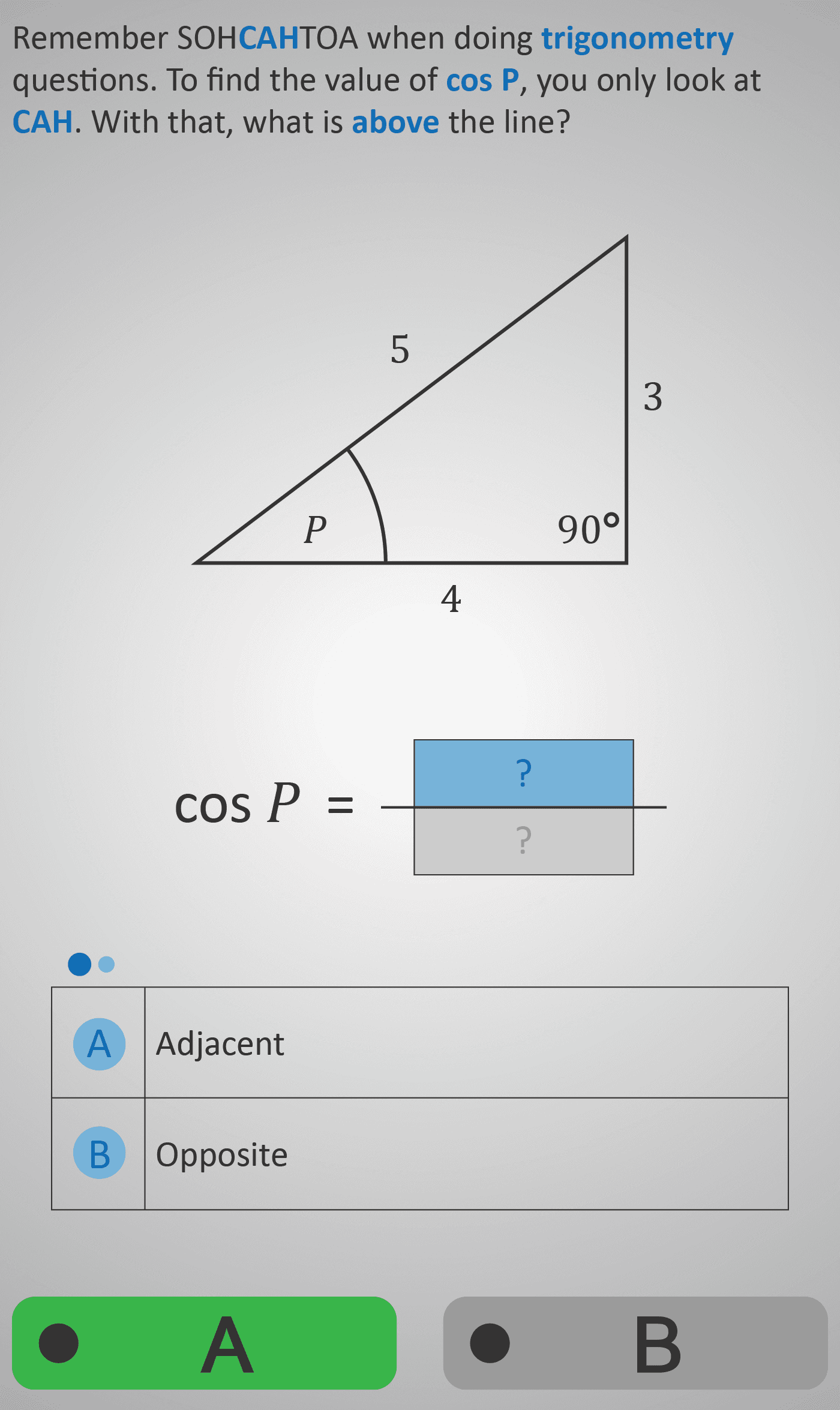
This lesson develops understanding of trigonometry using the SOHCAHTOA rule. Students learn to break down cosine, sine, and tangent into their component sides of a right-angled triangle.

For cos P, learners recall CAH, identifying the adjacent side above the line and the hypotenuse below the line.

For tan A, learners use TOA, placing the opposite side above and the adjacent side below.

For sin T, learners follow SOH, with the opposite side above and the hypotenuse below.

By focusing on which side is “above” and which is “below” in the fraction, students strengthen their understanding of ratios rather than memorising formulas mechanically. This set builds step-by-step reasoning: starting with identifying the correct side (adjacent, opposite, hypotenuse), then positioning it in the correct place for the ratio.

The worked diagrams (triangles with side lengths) guide visual recognition, while multiple-choice answers reinforce correct placement.

Step 1 / 6

Prerequisite Knowledge Required

Linked Phlows: Hyp–Adj–Opp 2 – identifying sides of a right-angled triangle relative to a given angle.
Pythagoras 2 – understanding the hypotenuse and side relationships.
Angles 2B – measuring and naming angles within triangles.

Main Category

Geometry & Trigonometry

Estimated Completion Time

Approx 6–10 seconds per question. 20 questions total. Total time: 2–4 minutes.

Cognitive Load / Step Size

Moderate — each screen isolates one trigonometric ratio, focusing on recognising side positions before combining them conceptually. The transitions between sine, cosine, and tangent are carefully spaced to minimise confusion and encourage retention through repetition.

Language & Literacy Demand

Moderate — mathematical symbols (sin, cos, tan) are supported with verbal scaffolding (“opposite over hypotenuse,” etc.). The layout and visual labels reduce linguistic complexity, though some new terminology (e.g., “adjacent”) may require brief reinforcement.

Clarity & Design

Excellent — clear diagrams of right-angled triangles highlight the relevant sides, with labels appearing in colour or shading to match the SOHCAHTOA formula being discussed. The “above” and “below” fraction structure directly supports ratio comprehension.

Curriculum Alignment

Irish Curriculum Strand: Geometry and Trigonometry

Recognise and label sides of a right-angled triangle relative to a given angle.
Define and apply the sine, cosine, and tangent ratios using SOHCAHTOA.
Understand trigonometric ratios as side-length relationships, not abstract formulas.
Prepare for solving problems involving missing sides or angles in right-angled triangles.

Engagement & Motivation

Moderate to High — the strong visual structure and clear cause-effect logic (e.g., “cos = adj/hyp”) keep students engaged. The connection between formula structure and triangle geometry makes the topic feel practical and learnable rather than abstract.

Error Opportunities & Misconceptions

Mixing up which side is “adjacent” versus “opposite.”
Forgetting that the hypotenuse is always opposite the right angle.
Confusing the placement of sides (above vs. below the line) in ratios.
Treating SOHCAHTOA as a memorisation rule rather than understanding its meaning.

Repetition with visual reinforcement reduces these errors effectively.

Transferability / Real-World Anchoring

Strong — trigonometry underpins navigation, engineering, and architecture. Even at this level, recognising ratios as relationships between sides sets the stage for applying trigonometry to heights, distances, and angle problems in real contexts.

Conceptual vs Procedural Balance

Conceptual-heavy — prioritises understanding of why each ratio has its structure before any calculation is introduced. Students learn the logic behind the formula, not just how to use it.

Learning Objectives Addressed

Identify the adjacent, opposite, and hypotenuse sides of a right-angled triangle.
Match the correct sides to sine, cosine, and tangent ratios using SOHCAHTOA.
Build conceptual understanding of trigonometric ratios as side-length relationships.
Prepare for applying trigonometric ratios in problem-solving and angle calculation.

What Your Score Says About You

Less than 5: Needs more practice distinguishing triangle sides and applying SOHCAHTOA correctly.
6–7: Understands most ratios but occasionally mixes up side placement.
8–9: Strong understanding of trigonometric relationships with minor recall slips.
10 / 10: Excellent mastery — confidently applies and explains SOHCAHTOA across all ratios.