Time 2

Overview

This set of exercises introduces proportional reasoning through real-world transport scenarios.

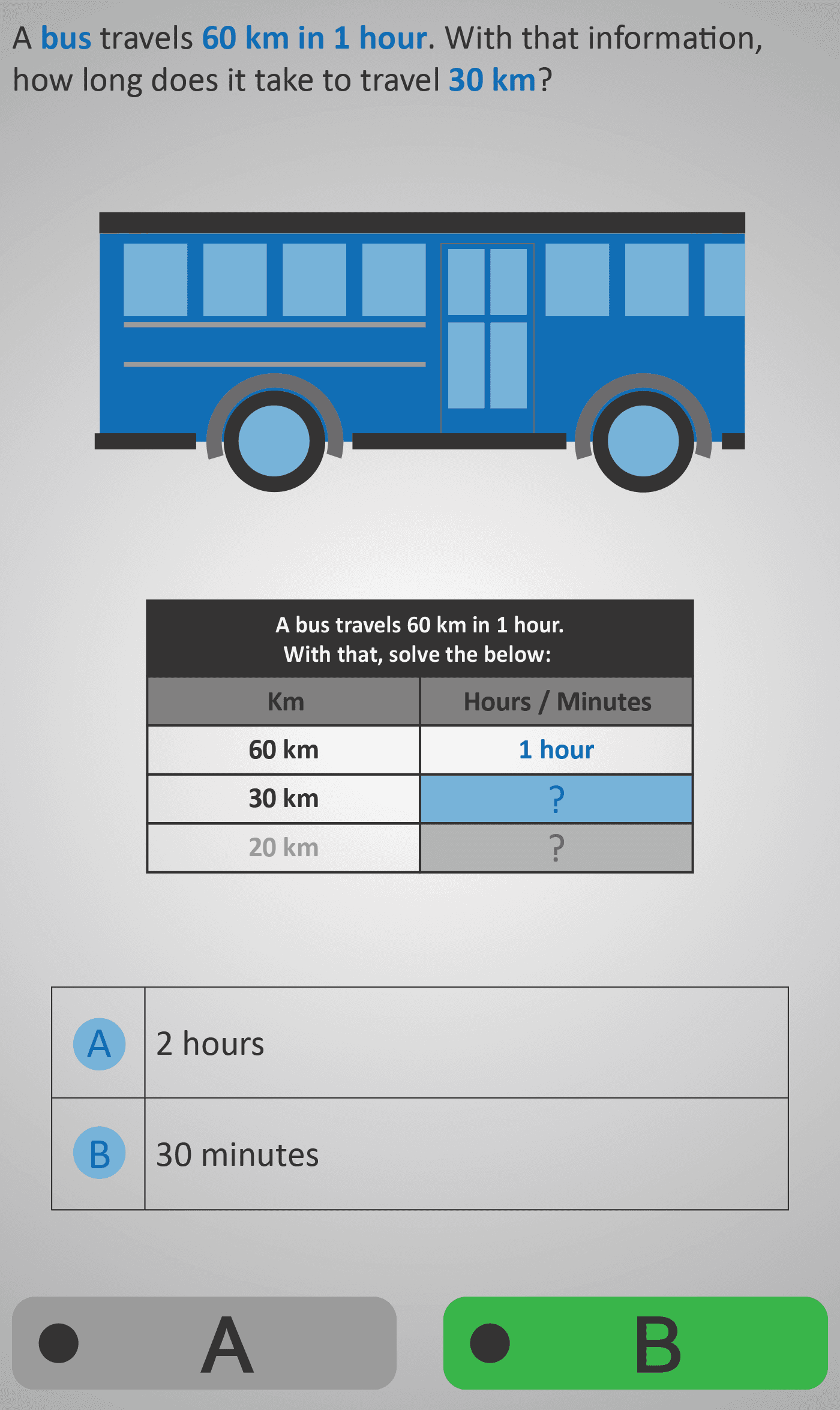
In the first problem, students are told that a bus travels 60 km in 1 hour. They are asked how long it would take the bus to travel 30 km. The options provided are 2 hours or 30 minutes, guiding students to realise that halving the distance halves the time.

The second problem extends this by asking for the travel time for 20 km. With the bus speed constant, students must work out that it takes 20 minutes, reinforcing the proportionality link between distance and time.

The third problem switches to a motorbike that travels 50 km in 1 hour. Students are asked how far it travels in 30 minutes, with options of 100 km or 25 km. They must identify that halving the time halves the distance.

Finally, the fourth problem builds on this with the same motorbike, asking how far it travels in 4 hours. The options given are 120 km or 200 km, and students must multiply the 1-hour distance (50 km) by 4 to reach the correct answer.

Together, these tasks help students develop fluency in applying ratios and unitary method thinking. By varying both distance and time across the questions, learners strengthen their understanding of direct proportion in practical contexts — a key stepping stone towards more formal speed, distance, and time equations.

Step 1 / 4

Prerequisite Knowledge Required

Linked Phlows: Multiply 2 – understanding multiplication and repeated addition.
Divide 2 – dividing quantities evenly and interpreting results.
Ratio 1 / Ratio 2 – recognising proportional relationships.
Time 1 – basic understanding of hours, minutes, and time measurement.

Main Category

Measurement – Speed, Distance & Time Relationships

Estimated Completion Time

Approx 6–10 seconds per question. 20 questions total. Total time: 2–4 minutes.

Cognitive Load / Step Size

Moderate — each step adds a proportional reasoning challenge (halving, doubling, or scaling by 4). The transition between bus and motorbike contexts introduces variety without increasing abstraction too quickly.

Language & Literacy Demand

Moderate — short problem statements with realistic contexts. Learners must interpret key numerical relationships but are supported by visual cues (icons or simple graphics) representing vehicles and distances.

Clarity & Design

Excellent — clear visuals (bus, motorbike, time arrows, or kilometre markers) illustrate proportional changes. The use of structured comparisons (e.g. “1 hour → 60 km” vs “30 mins → ?”) supports reasoning and makes relationships explicit.

Curriculum Alignment

Irish Curriculum Strand: Measures – Time, Speed, and Proportion

Explore relationships between distance, speed, and time.
Recognise and apply direct proportion in real contexts.
Use multiplication and division to solve rate-based problems.
Interpret time in minutes and hours for comparative calculations.

Engagement & Motivation

High — relatable travel contexts (bus, motorbike) make the maths feel practical. The real-world link to journeys and timetables promotes curiosity and helps students see the usefulness of proportional reasoning.

Error Opportunities & Misconceptions

Mixing up whether to multiply or divide when scaling.
Misinterpreting “half the time” as “half the speed.”
Forgetting to convert between minutes and hours.
Assuming all rates are constant without checking context.

Each example reinforces correct reasoning with clear numerical patterns to prevent confusion.

Transferability / Real-World Anchoring

Very Strong — directly connects to real-life experiences of travel, timetables, and distance estimation. Builds foundations for future work in physics, unit rate calculations, and ratio-based reasoning in exams.

Conceptual vs Procedural Balance

Balanced — combines conceptual understanding of direct proportion with procedural practice applying multiplication and division. The visual and contextual framing ensures both “why” and “how” are reinforced.

Learning Objectives Addressed

Understand how time and distance are linked when speed is constant.
Apply proportional reasoning to scale up or down correctly.
Use multiplication and division to solve speed–distance–time problems.
Strengthen fluency with real-world quantitative reasoning.

What Your Score Says About You

Less than 5: Needs more work distinguishing when to multiply vs divide in proportion problems.
6–7: Understands the proportional idea but may make unit or direction errors.
8–9: Accurately applies proportional reasoning in most cases.
10 / 10: Excellent mastery — confidently links distance, speed, and time across varied contexts.