Visual Algebra 2A
Overview
This Phlow introduces students to the idea of multiplying variables using visual representations. Instead of abstract symbols alone, dots are used to represent values of variables, helping learners see how multiplication works step by step.
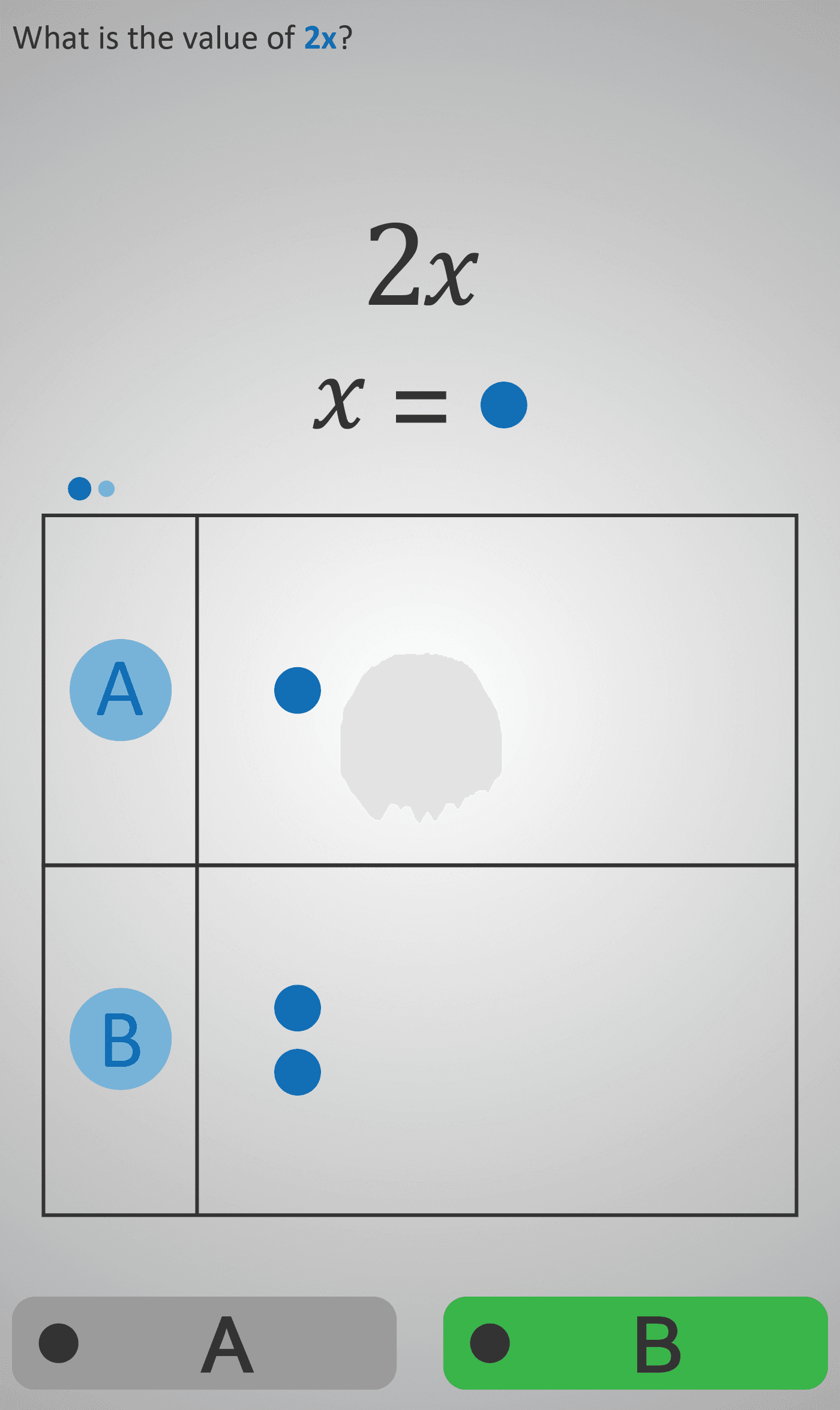
In the first two screens, students explore the expression 2x. When x is represented by one circle, doubling it means 2x equals two circles. The activity reinforces the idea that multiplication is repeated addition.
Students are then asked, “How many circles are equal to 2x?” to connect the visual model with the symbolic notation.
The next two screens extend this to 3a. If a is represented by three circles, then 3a means three groups of three circles, totalling nine. Learners visually match this with the algebraic expression.
By the end, students can confidently recognise that multiplying variables by numbers follows the same logic as multiplying ordinary numbers, but with variables represented symbolically.
This Phlow builds a strong foundation for algebra by combining visual reasoning with symbolic notation, helping students bridge the gap between concrete understanding and abstract algebraic thinking.
Prerequisite Knowledge Required
- Linked Phlows: Algebra 1A–1C – recognising variables and simple expressions.
- Multiply 1 / Multiply 2 – understanding multiplication as repeated addition.
- Visual Patterns 1 – recognising groups and repeated quantities visually.
Main Category
Algebra – Visual Modelling and Symbolic Reasoning
Estimated Completion Time
Approx 6–10 seconds per question. 20 questions total. Total time: 2–4 minutes.
Cognitive Load / Step Size
Low to Moderate — the use of dots and visual grouping lowers abstraction, allowing learners to grasp the link between repeated addition and algebraic multiplication. Each new example increases complexity gradually (2x → 3a).
Language & Literacy Demand
Low — the text is minimal and supported heavily by visuals. Learners focus on interpreting diagrams rather than decoding written algebraic explanations, making it accessible for those with weaker reading skills.
Clarity & Design
Excellent — simple dot arrays and labelled expressions ensure clarity. The visuals directly mirror the algebraic statements, reinforcing comprehension. Minimal visual clutter keeps attention on the relationship between images and symbols.
Curriculum Alignment
Irish Curriculum Strand: Algebra – Representing Patterns and Relationships
- Recognise multiplication as repeated addition.
- Interpret algebraic expressions using visual representations.
- Connect visual models (e.g., dot arrays) to symbolic algebra (e.g., 2x, 3a).
- Understand the meaning of coefficients in algebraic terms.
Engagement & Motivation
High — visual learning makes the abstract concept of algebra feel intuitive. The dot-based representations and colour contrasts maintain focus and reduce intimidation often associated with algebraic symbols.
Error Opportunities & Misconceptions
- Miscounting visual groups or failing to connect them to the written expression.
- Confusing the coefficient (number) with the variable itself.
- Believing variables must have numeric values rather than symbolic meaning.
The sequence’s repetition and alternating visual-symbolic cues effectively correct these misconceptions.
Transferability / Real-World Anchoring
Moderate — though algebraic, this visual foundation transfers to understanding area models, scaling, and proportional reasoning. It builds readiness for real-world algebraic problem-solving in later Phlows.
Conceptual vs Procedural Balance
Conceptual — the Phlow focuses on why multiplication of variables works, not just how. Students form mental connections between the visual quantity and the algebraic expression, developing true understanding before symbolic fluency.
Learning Objectives Addressed
- Recognise variables as placeholders for quantities.
- Understand coefficients as multipliers of variables.
- Relate visual groupings to algebraic notation (e.g., 2x = two groups of x).
- Strengthen conceptual bridges between arithmetic and algebra.
What Your Score Says About You
- Less than 5: Needs more practice connecting symbols with visual quantities.
- 6–7: Understands multiplication visually but sometimes misreads algebraic notation.
- 8–9: Accurately links visuals with algebraic meaning in most examples.
- 10 / 10: Excellent mastery — confidently interprets and represents algebraic multiplication both visually and symbolically.