Algebra 3A
Overview
Guides learners through the process of multiplying out brackets using the distributive property in algebra. The exercise breaks the process into small, interactive steps, ensuring that each part of the expansion is understood before moving on.
Step 1: Multiply the First Term
Students begin with the expression 2(3x − 4y). They first multiply 2 × 3x, selecting the correct term 6x. This reinforces the rule that the number outside the brackets multiplies each term inside.
Step 2: Identify the Sign
Learners identify whether the sign between the terms is plus or minus, recognising that since the second term inside the bracket is negative, the correct sign is −.
Step 3: Multiply the Second Term
Finally, students multiply 2 × 4y to get 8y, completing the full expansion: 2(3x − 4y) = 6x − 8y.
Each step is supported by simple visuals and colour cues highlighting active parts of the equation. The design scaffolds learning, moving from individual term multiplication to the full expanded form. By the end, students clearly understand how to apply the distributive law to algebraic expressions, maintaining correct signs and coefficients throughout.
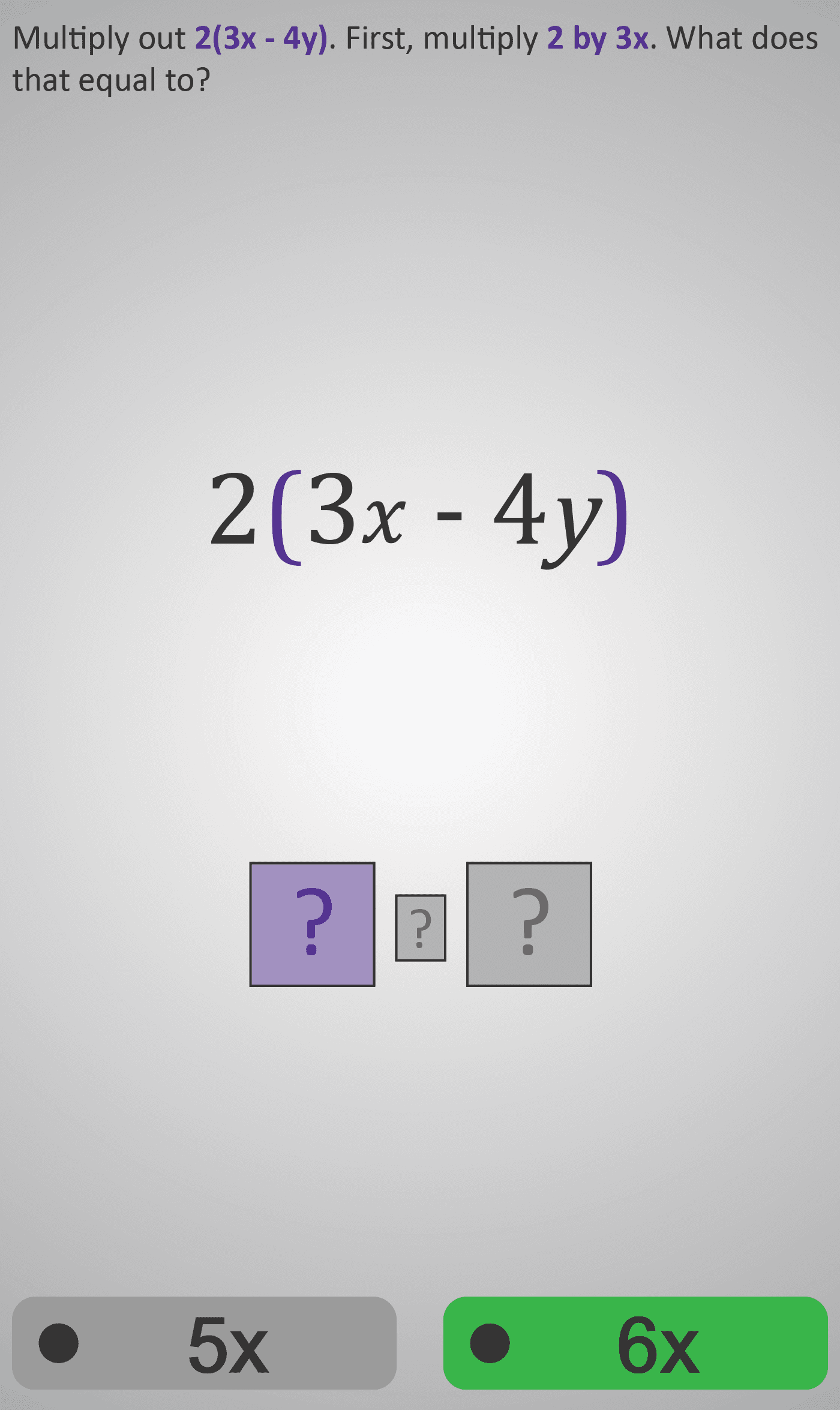
Prerequisite Knowledge Required
- Linked Phlows: Visual Algebra 2A – multiplying variables by numbers.
- Visual Algebra 2B – combining variables and constants using addition.
- Brackets 2 – recognising expressions with brackets.
- Signs 2 – understanding positive and negative terms.
Main Category
Algebra – Expanding Brackets
Estimated Completion Time
Approx 8–12 seconds per question. 30 questions total. Total time: 4–6 minutes.
Cognitive Load / Step Size
Moderate — each step isolates one small part of the expansion (first multiplication, sign, second multiplication). The progression prevents overload while reinforcing accuracy through repetition and pattern recognition.
Language & Literacy Demand
Low — concise instructions use consistent phrasing (“multiply,” “next sign,” “what does that equal to?”). Highlighted keywords (e.g., multiply, minus) support understanding without excessive text.
Clarity & Design
Excellent — the bracketed expression is displayed clearly at the top of each screen, with purple highlighting for the term currently being worked on. Grey and green buttons focus learner attention, and each stage visibly builds toward the final expanded form.
Curriculum Alignment
Irish Curriculum Strand: Algebra – Expressions, Equations, and Relationships
- Apply the distributive law to expand expressions of the form a(b ± c).
- Correctly handle positive and negative terms within brackets.
- Multiply coefficients with variables systematically.
- Write simplified, fully expanded algebraic expressions.
Engagement & Motivation
High — the progressive, puzzle-like design helps learners feel successful at each stage. Immediate visual feedback reinforces correct reasoning and builds confidence in tackling algebraic problems.
Error Opportunities & Misconceptions
- Forgetting to multiply the second term by the number outside the brackets.
- Mixing up signs (e.g., changing − to +).
- Ignoring coefficients when variables are present.
The step-by-step Phlow addresses each of these common errors individually, ensuring mastery before moving to full expansions.
Transferability / Real-World Anchoring
Moderate — while algebraic, the concept underpins many real-world applications (area formulas, proportional reasoning, physics equations). Understanding distribution prepares students for solving equations and simplifying expressions in later topics.
Conceptual vs Procedural Balance
Balanced — the process is procedural but underpinned by clear conceptual links (distribution applies to both terms, signs carry through). The visual design makes the abstract rule concrete.
Learning Objectives Addressed
- Expand brackets using the distributive law.
- Multiply coefficients and variables correctly.
- Apply negative and positive signs accurately.
- Write simplified, expanded expressions with confidence.
What Your Score Says About You
- Less than 5: Needs more practice recognising how each term in brackets is affected by the multiplier.
- 6–7: Understands the distributive law but may mix up signs.
- 8–9: Accurately multiplies terms and signs consistently.
- 10 / 10: Excellent understanding — confidently expands any simple algebraic bracket.