Algebra 3G
Overview
Helps students understand how to find the value of x in simple linear equations through a clear, visual, and guided process. The lesson builds procedural confidence while reinforcing the concept of balance — whatever is done to one side of the equation must be done to the other.
Step 1: Move the Constant
Learners start with an equation such as 3x + 5 = 20 and are prompted to separate x-terms and numbers by moving +5 to the other side, changing it to −5.
Step 2: Simplify Both Sides
Simplify the right-hand side to get 3x = 15.
Step 3: Isolate x
Decide whether to multiply or divide to find x, recognising that x = 15 ÷ 3, and conclude that x = 5.
Each step isolates one cognitive action — first identifying what changes sign, then applying inverse operations. The use of sequential dots and progressive simplification mirrors real algebraic reasoning. The learner actively participates by selecting the correct operation, reinforcing both conceptual and procedural understanding.
By the end, students can confidently solve one-step and two-step equations and explain why sign changes occur across the equals sign — a foundation for more advanced algebraic manipulation in future levels.
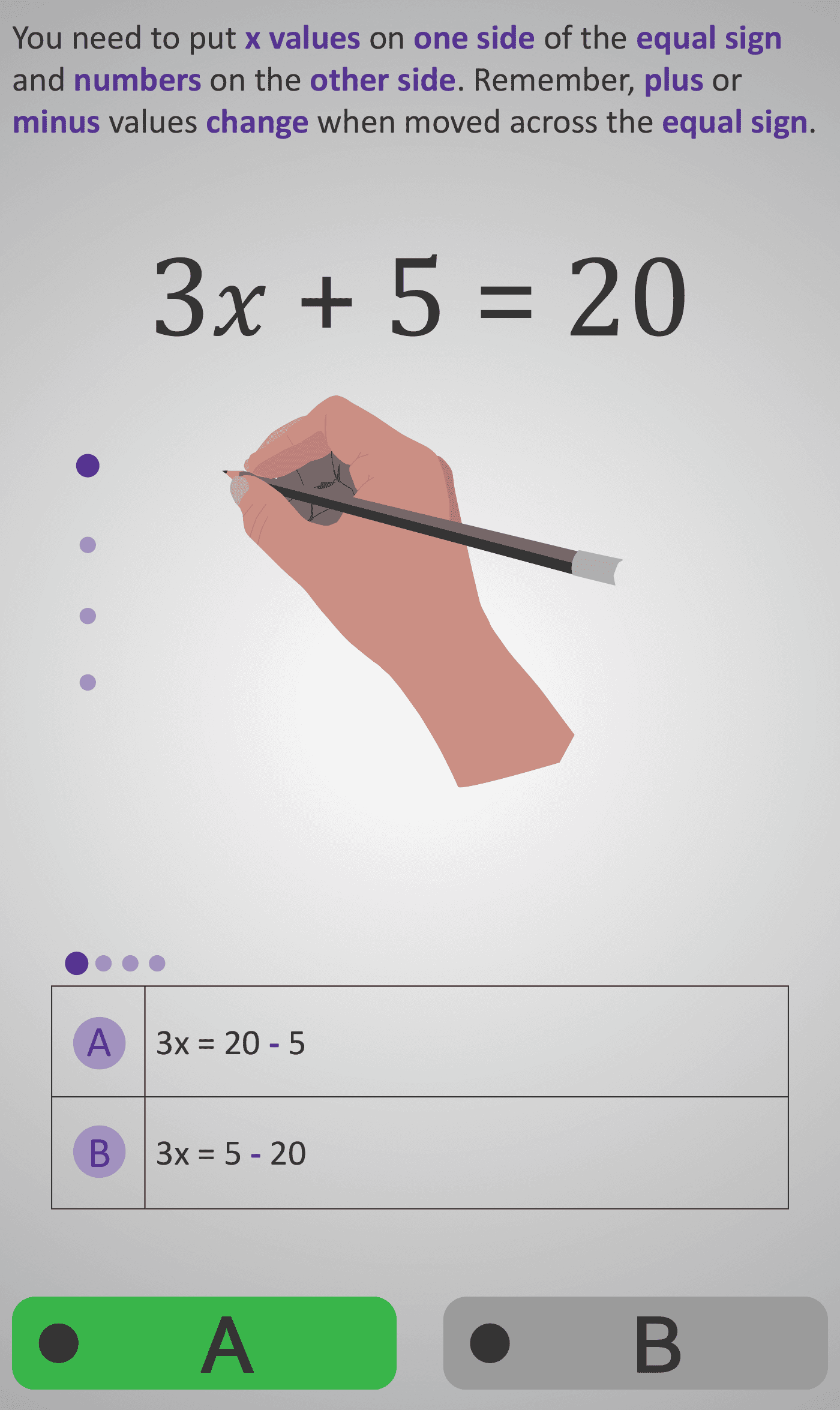
Prerequisite Knowledge Required
- Linked Phlows: Algebra 3F – expanding and simplifying expressions with brackets.
- Algebra 3E – simplifying expressions by combining like terms.
- Add & Sub 3 – adding and subtracting positive and negative numbers.
- Multiply & Divide 2 – basic multiplication and division facts.
Main Category
Algebra – Equations and Relationships
Estimated Completion Time
Approx 10–15 seconds per screen. 4 screens × ~12 seconds ≈ 1–2 minutes total.
Cognitive Load / Step Size
Moderate — only one operation or transformation per step (move a term, simplify, divide). The process is chunked to reduce cognitive demand and highlight inverse relationships clearly.
Language & Literacy Demand
Low — each instruction is concise and follows a predictable pattern (“Move…”, “Simplify…”, “What does x equal to?”). Key words (equals, plus, minus, divide) are emphasised in purple to strengthen algebraic vocabulary.
Clarity & Design
Excellent — clean, uncluttered visuals; the equals sign remains central to maintain symmetry and conceptual balance. The animated hand reinforces the action of writing and thinking procedurally.
Curriculum Alignment
Irish Curriculum Strand: Algebra – Expressions, Equations and Relationships
- Recognise and apply inverse operations when solving equations.
- Maintain equality when performing operations on both sides of an equation.
- Interpret solutions as the value of the variable that makes both sides equal.
Engagement & Motivation
High — students immediately see the effect of each step on both sides of the equation. The progressive reveal and check-for-understanding format sustain focus and create a sense of problem-solving flow.
Error Opportunities & Misconceptions
- Forgetting to change + to – (or vice versa) when moving terms.
- Incorrectly performing operations on only one side.
- Confusing multiplication with division when isolating x.
The Phlow anticipates these by separating each operation and confirming understanding before proceeding.
Transferability / Real-World Anchoring
Strong — solving simple equations underpins a wide range of contexts, from financial calculations to physics formulas and coding logic. The balance concept applies across all problem-solving domains.
Conceptual vs Procedural Balance
Balanced — students practise a clear procedure but also internalise the concept of maintaining equality and applying inverse operations, not just “moving numbers.”
Learning Objectives Addressed
- Isolate x by applying inverse operations.
- Change sign correctly when transposing terms.
- Maintain equality while simplifying.
- Strengthen confidence in equation solving.
What Your Score Says About You
- Below 5: Beginning — needs more practice with moving terms and inverse operations.
- 5–7: Developing — understands balance but may confuse sign changes.
- 8–9: Proficient — applies steps correctly with minor errors.
- 10 / 10: Mastery — can independently solve and explain simple equations with confidence.