Arrow Diagram 3
Overview
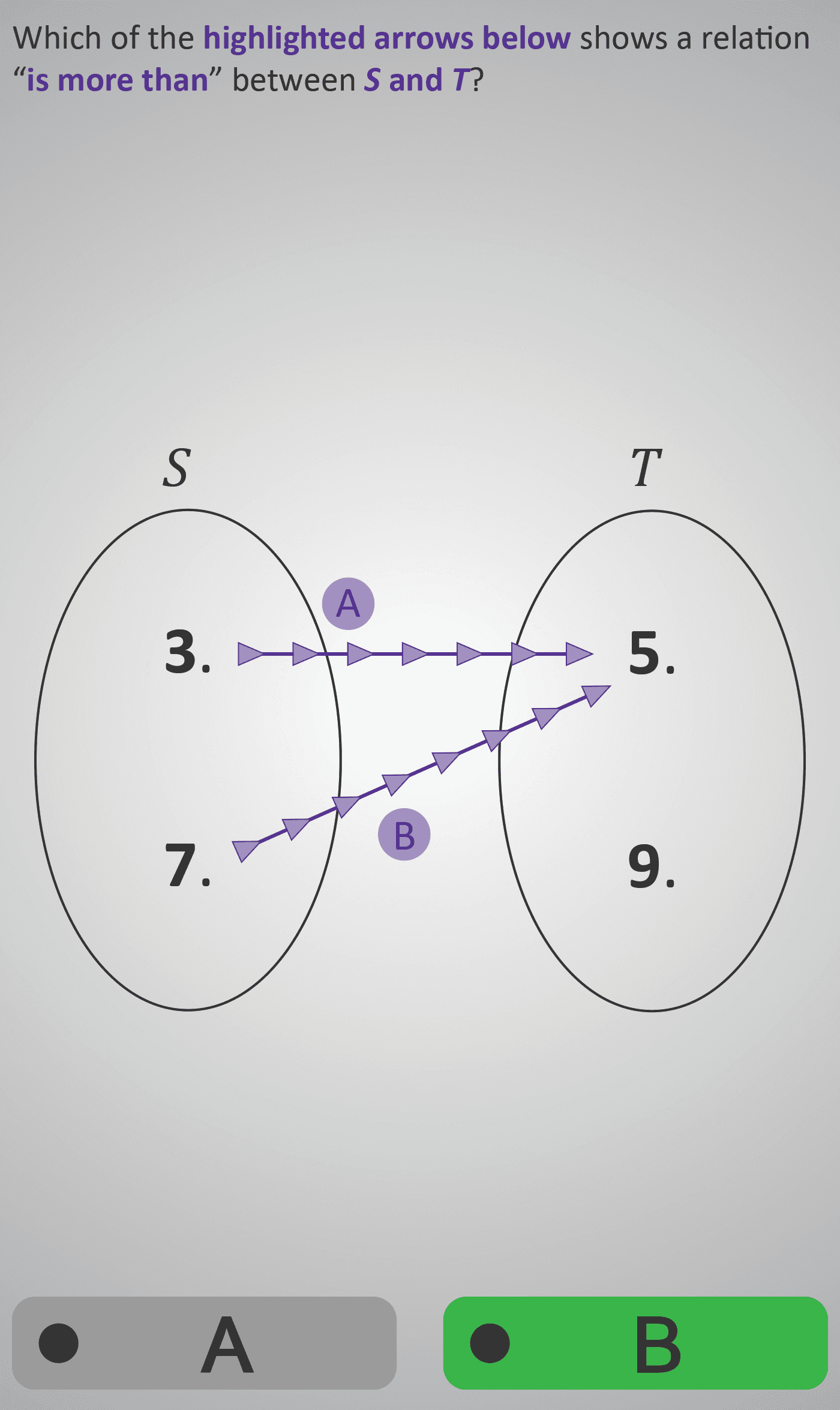
This Phlow develops understanding of relations between sets using arrow diagrams. Learners are introduced to two sets, S and T, each containing numbers. Arrows are used to show relationships such as “is more than” between elements in the two sets.
Students must determine which direction of arrows correctly represents this relation — for example, an element in S pointing to a smaller element in T. As the activity progresses, students practise reading and forming ordered pairs (couples) from the diagrams, identifying which number in S connects to which number in T.
By the end, learners understand that an arrow diagram visually represents relationships and that these relationships can be written symbolically as ordered pairs, e.g. (7, 5), meaning “7 is more than 5.” This Phlow bridges visual reasoning and formal set notation, preparing students for future topics in functions and mappings.
Prerequisite Knowledge Required
- Arrow Diagram 2 – Representing relations between two sets.
- Number 2B – Understanding greater than and less than.
- Sets 1A – Identifying elements and members of a set.
Main Category
Relations & Functions – Arrow Diagrams
Estimated Completion Time
Approx. 10–12 seconds per question (30 questions total). Total Time: 6–7 minutes.
Cognitive Load / Step Size
Moderate — learners interpret multiple visual elements (arrows, sets, labels), but each step isolates a single comparison or relation. The gradual introduction of ordered pairs supports working memory and reinforces understanding through repetition.
Language & Literacy Demand
Moderate — key phrases like “is more than” and “couple created” are explicitly highlighted and repeated. Sentence structures are simple, direct, and supported visually to aid comprehension.
Clarity & Design
The layout supports visual reasoning and focus:
- Consistent purple highlights guide attention to correct arrows.
- Greyed-out distractor arrows clarify which relationships are valid.
- Progressive sequence: select → reason → record pair.
- Dual-column diagram reinforces mapping structure (Set S → Set T).
Curriculum Alignment
Irish Junior Cycle Mathematics:
- Strand 3 – Algebra: Represent and interpret relations between sets of numbers.
- Strand 4 – Functions: Understand that a function can be represented as a set of ordered pairs.
- Learning Outcome 3.8: “Interpret and represent relationships in diagrammatic form.”
Engagement & Motivation
By turning abstract relations into visual, interactive reasoning, learners actively discover how each comparison creates a logical connection. The “couple” table at the end adds a puzzle-like challenge, enhancing curiosity and flow.
Error Opportunities & Misconceptions
- Reversing arrow direction (“less than” vs “more than”).
- Mixing up which set corresponds to the first or second element in an ordered pair.
- Assuming every element must connect to all others.
These are addressed visually through immediate feedback, consistent highlighting, and repetition of relational logic.
Transferability / Real-World Anchoring
High — understanding relations underpins graphing functions, comparing data, and logical reasoning in computer science (mapping inputs to outputs). This concept supports mathematical modelling and algorithmic thinking.
Conceptual vs Procedural Balance
Balanced — learners develop conceptual understanding (“what does ‘is more than’ mean?”) while practising procedural representation (drawing arrows, listing pairs). Both skills reinforce each other to form a deep grasp of relational logic.
Learning Objectives Addressed
- Interpret arrow diagrams showing number relationships between two sets.
- Identify correct directional relationships for “is more than.”
- Represent relationships as ordered pairs.
- Strengthen understanding of how sets and relations connect in algebraic thinking.
What Your Score Says About You
- Less than 5: You may be reversing the relation or mixing up which set comes first — review how “is more than” points from larger to smaller values.
- 6–7: You understand direction but might need to double-check pair notation.
- 8–9: You can confidently interpret and record relations correctly.
- 10 / 10: Excellent — you fully understand how arrow diagrams show and record relationships between sets.