Central Symmetry 3A
Overview
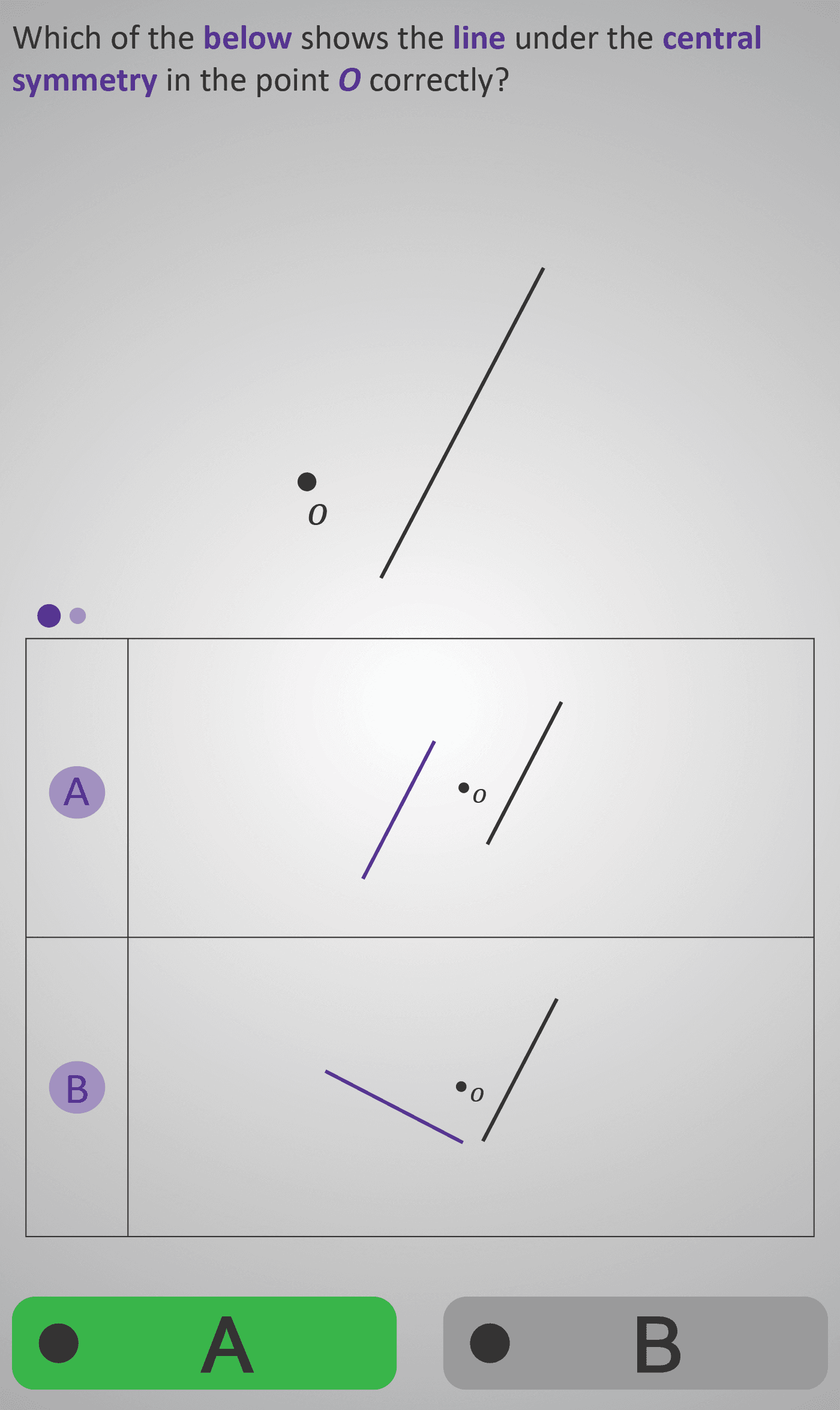
In this Phlow, students build an understanding of central (point) symmetry, where a shape is transformed by rotating it 180° around a central point O. The line is first reflected through O without labels, then learners identify how its image appears opposite O, keeping the same orientation but mirrored in position.
They then explore how labelling affects symmetry — the ends of the line swap positions (e.g., c ↔ d) because each point reflects through O to its opposite side. Next, students apply the same logic to two joined lines, noticing that each segment and vertex must be directly opposite its original across O. Through visual reasoning and multiple-choice interaction, learners confirm the correct mirrored positioning and orientation of figures under central symmetry.
Prerequisite Knowledge Required
- Symmetry 2A – Recognising mirror (axial) symmetry.
- Geometry 2B – Identifying lines, angles, and points.
- Transformations 2C – Understanding reflections and rotations.
Main Category
Geometry – Transformations (Symmetry & Reflection)
Estimated Completion Time
Approx. 8–12 seconds per question (30 questions total). Total Time: 4–6 minutes.
Cognitive Load / Step Size
Moderate — each step adds one new cognitive challenge: first the visual flip, then labelled ends, then multi-line figures. This incremental structure maintains flow and prevents overload while keeping curiosity high.
Language & Literacy Demand
Low — concise sentences and highlighted mathematical terms (central symmetry, line, point O) enable comprehension through visuals rather than dense reading. Ideal for mixed-ability learners or those with emerging literacy.
Clarity & Design
- Black and purple colour coding clearly distinguishes the original figure and its image.
- Labels (c, d, e, q, w) help learners track each reflected point.
- Central point O remains constant across screens, anchoring visual reasoning.
- Clean, functional graphics focus attention on transformation rather than decoration.
Curriculum Alignment
Irish Junior Cycle Mathematics:
- Strand 3 – Geometry and Trigonometry.
- Learning Outcome 3.2 – “Recognise and describe geometric transformations, including translations, rotations, reflections, and central symmetry.”
- Learning Outcome 3.3 – “Understand and apply the properties of symmetry in geometrical figures.”
Engagement & Motivation
The Phlow feels like a visual puzzle — students experiment, predict, and confirm outcomes through pattern recognition. The short, binary-choice format (A or B) keeps decisions quick and feedback immediate, sustaining engagement and flow.
Error Opportunities & Misconceptions
- Confusing central symmetry with mirror symmetry (reflecting across a line rather than through a point).
- Reversing orientation incorrectly — flipping the line instead of rotating around O.
- Forgetting that labelled points (e.g., c and d) swap sides.
Each misconception is addressed through side-by-side comparison and corrective visual reinforcement.
Transferability / Real-World Anchoring
High — central symmetry underpins design, pattern creation, engineering, and computer graphics. It also prepares learners for coordinate transformations and 180° rotations in higher-level geometry and algebra.
Conceptual vs Procedural Balance
Strongly conceptual — learners visualise and reason geometrically rather than follow memorised procedures. Later Phlows introduce formal coordinate methods built on this conceptual base.
Learning Objectives Addressed
- Understand that central symmetry reflects each point through a centre to its opposite position.
- Identify correctly reflected lines and labels under central symmetry.
- Distinguish between central and mirror (axial) symmetry.
- Apply geometric reasoning to multi-line shapes and figures.
What Your Score Says About You
- Less than 5: You may be confusing line symmetry with point symmetry — try visualising a half-turn around O.
- 6–7: You understand the idea but sometimes miss label swaps or reversed orientations.
- 8–9: You reason spatially and consistently identify the correct symmetric image.
- 10 / 10: Excellent — you can visualise central symmetry with precision and are ready for coordinate-based applications.