Central Symmetry 3B
Overview
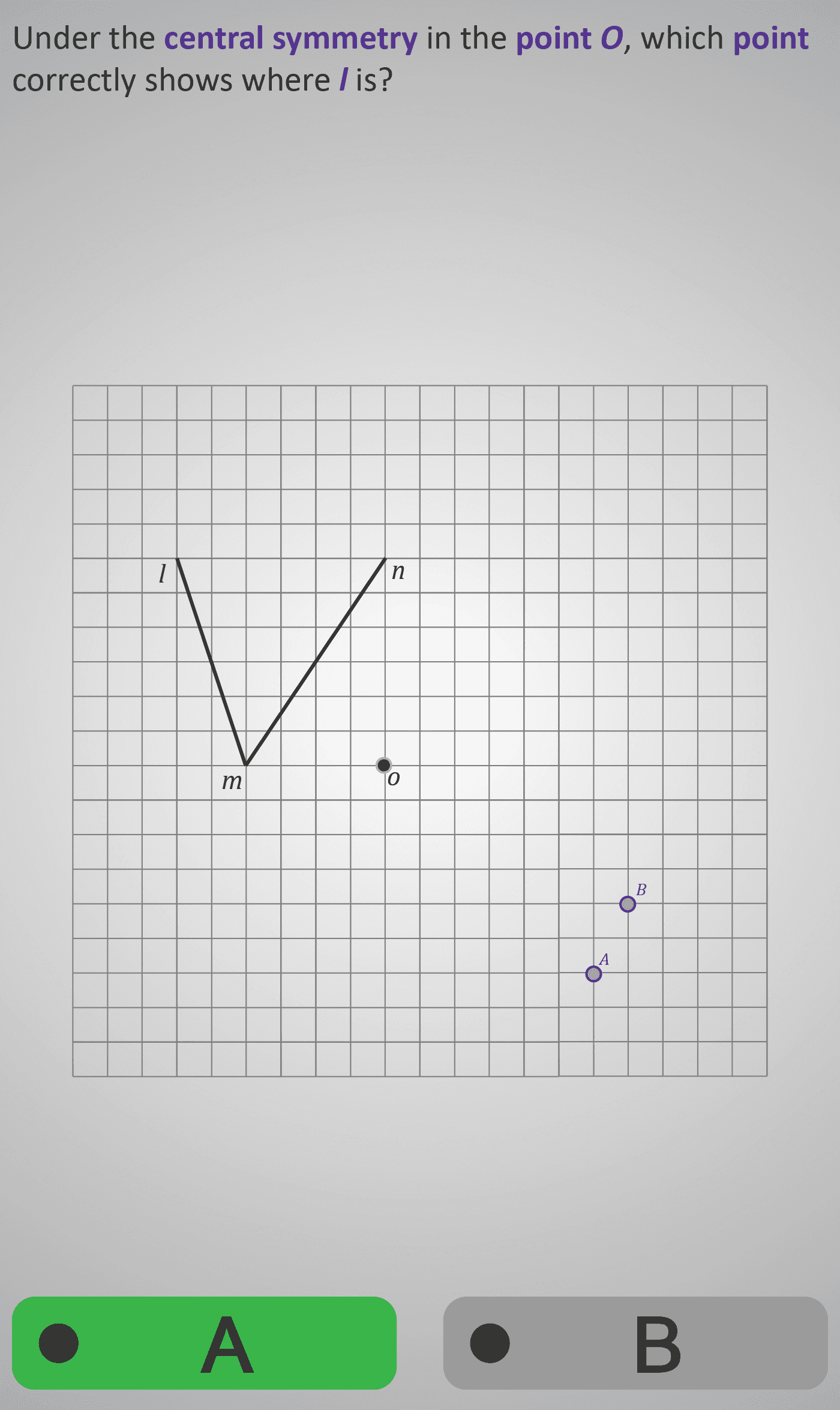
In this Phlow, students move from abstract visualisations of symmetry to precise geometric positioning using a coordinate grid. The task centres on a “V”-shaped figure labelled l, m, n with a fixed central point O.
Learners identify, step-by-step, the correct image of each vertex under central symmetry about O. By analysing the grid, they see that each new point lies directly opposite its original, maintaining equal distance from O but in the reverse direction.
Each question isolates one vertex (first l, then m, then n) to focus reasoning on the logic of transformation rather than the entire shape. Gradually, students reconstruct the complete symmetric figure, reinforcing the rule that central symmetry is equivalent to a 180° rotation around a point.
This Phlow bridges visual intuition and geometric calculation, showing how symmetry can be represented concretely on grids — a key foundation for transformations in coordinate geometry.
Prerequisite Knowledge Required
- Central Symmetry 3A – Reflecting lines through a central point.
- Geometry 2B – Identifying points and lines on grids.
- Transformations 2C – Understanding reflections and equal distances.
- Measurement 2A – Counting units on a grid accurately.
Main Category
Geometry – Transformations (Symmetry & Coordinates)
Estimated Completion Time
Approx. 8–12 seconds per question (30 questions total). Total Time: 4–6 minutes.
Cognitive Load / Step Size
Moderate — each screen isolates a single vertex, allowing students to reason about one transformation at a time. The build-up from individual points to full shapes keeps the cognitive load low while steadily reinforcing geometric logic.
Language & Literacy Demand
Low — questions are concise, visual, and supported by labelled grids. Minimal text means students focus on where points move rather than decoding written instructions. Ideal for visual or kinesthetic learners.
Clarity & Design
- Coordinate grid supports accurate distance and orientation tracking.
- Labels (l, m, n, O) remain consistent across all screens.
- Original shape shown in black; reflected image in purple for instant comparison.
- Minimalist layout maintains focus and precision.
- Progressive reveal (point-by-point) builds curiosity and problem-solving engagement.
Curriculum Alignment
Irish Junior Cycle Mathematics:
- Strand 3 – Geometry and Trigonometry.
- Learning Outcome 3.2 – “Recognise and describe transformations (translation, rotation, reflection, and central symmetry) using grids and coordinates.”
- Learning Outcome 3.3 – “Use coordinate grids to explore and represent symmetry.”
Engagement & Motivation
The grid puzzle format turns symmetry into a spatial challenge. Students visualise, estimate, and verify — gaining satisfaction from precise placement. The interactivity sustains flow and appeals to learners who enjoy logical, hands-on problem solving.
Error Opportunities & Misconceptions
- Reflecting across the wrong axis (treating it as mirror symmetry instead of point symmetry).
- Moving the point the correct distance but in the wrong direction.
- Miscounting squares on the grid (especially diagonal positions).
- Forgetting that every vertex moves through O to the opposite side.
Each question isolates and corrects one misconception at a time through visual feedback and reinforcement.
Transferability / Real-World Anchoring
High — spatial reasoning here applies to map reading, design, CAD systems, and robotics. This Phlow strengthens mental rotation and geometric visualisation skills crucial for advanced STEM learning.
Conceptual vs Procedural Balance
Balanced — learners develop conceptual understanding (that central symmetry is a half-turn) alongside procedural fluency (plotting points precisely on a grid). Both reasoning and execution are reinforced throughout.
Learning Objectives Addressed
- Identify symmetric points under central symmetry on a coordinate grid.
- Understand that each point lies the same distance from the centre in the opposite direction.
- Apply reasoning to reconstruct the entire symmetric image.
- Develop spatial accuracy for transformations in coordinate geometry.
What Your Score Says About You
- Less than 5: You may be reflecting across a line — remember, central symmetry moves points through O.
- 6–7: You understand the idea but sometimes misplace points diagonally — check equal distances carefully.
- 8–9: Strong grasp of symmetry; any errors likely due to counting accuracy.
- 10 / 10: Excellent — you can visualise and apply 180° rotations accurately, ready for coordinate rule-based transformations ((x, y) → (−x, −y)).