Co-ordinate 3A

Overview

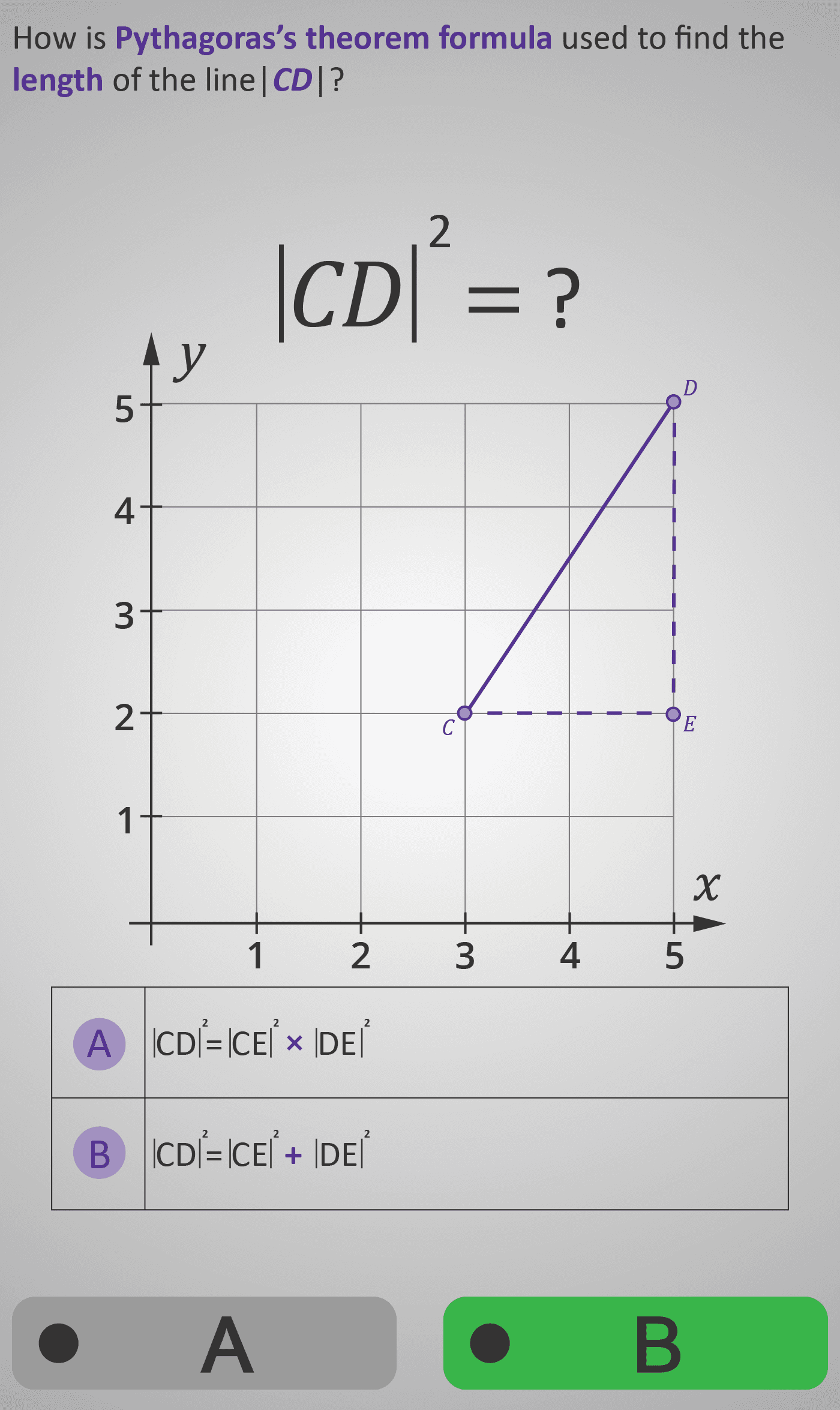
This Phlow introduces how Pythagoras’s theorem can be applied in coordinate geometry. Students explore the right-angled triangle formed between two points, C(x₁, y₁) and D(x₂, y₂). By dropping perpendiculars, they see that the horizontal and vertical “gaps” (Δx and Δy) form the two shorter sides of the triangle:

|CD|² = |CE|² + |DE|²

Across a sequence of guided steps, learners practise writing the relationship, substituting values from the grid, and combining them to find the diagonal length of |CD|. Visual reasoning transitions smoothly into algebraic thinking, showing how Pythagoras’s theorem leads directly to the distance formula.

The Phlow develops spatial reasoning, precision in grid reading, and understanding of squared relationships — forming a bridge between visual geometry and coordinate algebra.

Step 1 / 3

Prerequisite Knowledge Required

Co-ordinate 2B – Reading and plotting points on a grid.
Right Triangles 2A – Basics of Pythagoras’s theorem.
Understanding right-angled triangles and squaring numbers.
Ability to read x- and y-coordinates accurately.
Familiarity with “horizontal” and “vertical” distance terminology.

Main Category

Geometry & Coordinate Algebra

Estimated Completion Time

Approx. 8–12 seconds per question (30 questions total). Total Time: 4–6 minutes.

Cognitive Load / Step Size

Moderate — each step isolates one sub-operation (find Δx, find Δy, square, add, take square root). The clear diagram-to-formula progression ensures conceptual integration before abstraction. Step size is carefully tuned to maintain flow without overloading working memory.

Language & Literacy Demand

Low to moderate — notation such as |CD| and exponents (²) are central but supported by strong visual scaffolds. Minimal text reduces reading demand, and key terms (“gap,” “length,” “equal”) are colour-highlighted for clarity.

Clarity & Design

High-contrast grid with dashed right-angle triangle emphasises relationships.
Purple lines trace Δx and Δy before forming the hypotenuse |CD|.
Step-by-step animation connects diagram, numbers, and symbolic representation.
Labels and point markers (C, D, E) maintain consistent spatial logic.

Curriculum Alignment

Irish Junior Cycle Mathematics:

Strand 3 – Geometry and Trigonometry
Learning Outcomes:

Apply Pythagoras’s theorem to calculate lengths in right-angled triangles.
Represent and interpret geometric relationships on coordinate grids.
Develop algebraic reasoning by generalising geometric patterns.

Engagement & Motivation

Students are actively engaged by visual reasoning tasks that reveal the logic behind the distance formula. The “discover-then-calculate” structure delivers small successes at each step, building confidence and curiosity for abstract coordinate work.

Error Opportunities & Misconceptions

Mixing up Δx and Δy (horizontal vs vertical gap).
Forgetting to square before adding.
Failing to take the square root after summing squares.
Misinterpreting |CD| as a subtraction rather than distance.

The Phlow addresses each through visual contrast and guided correction (e.g. colour change cues when squaring or taking the root).

Transferability / Real-World Anchoring

High — understanding distance on a grid links directly to navigation, mapping, design, and physics. The concept forms the foundation for vectors, gradients, and spatial measurement in later studies.

Conceptual vs Procedural Balance

Strongly conceptual — learners explore why Pythagoras’s theorem works geometrically before performing calculations. Procedural fluency naturally follows from visual comprehension.

Learning Objectives Addressed

Identify horizontal and vertical gaps between two points on a coordinate grid.
Apply Pythagoras’s theorem to find diagonal (line) length.
Relate geometric distance to coordinate difference.
Build toward deriving the general distance formula.

What Your Score Says About You

Less than 5: Revisit Pythagoras’s theorem or practise identifying coordinate gaps.
6–7: Solid understanding — review squaring and root-taking steps for accuracy.
8–9: Excellent reasoning; minor errors may stem from grid precision.
10 / 10: Outstanding! You can confidently apply Pythagoras to coordinate problems — ready for gradients and midpoints next.