Co-ordinate 3B
Overview
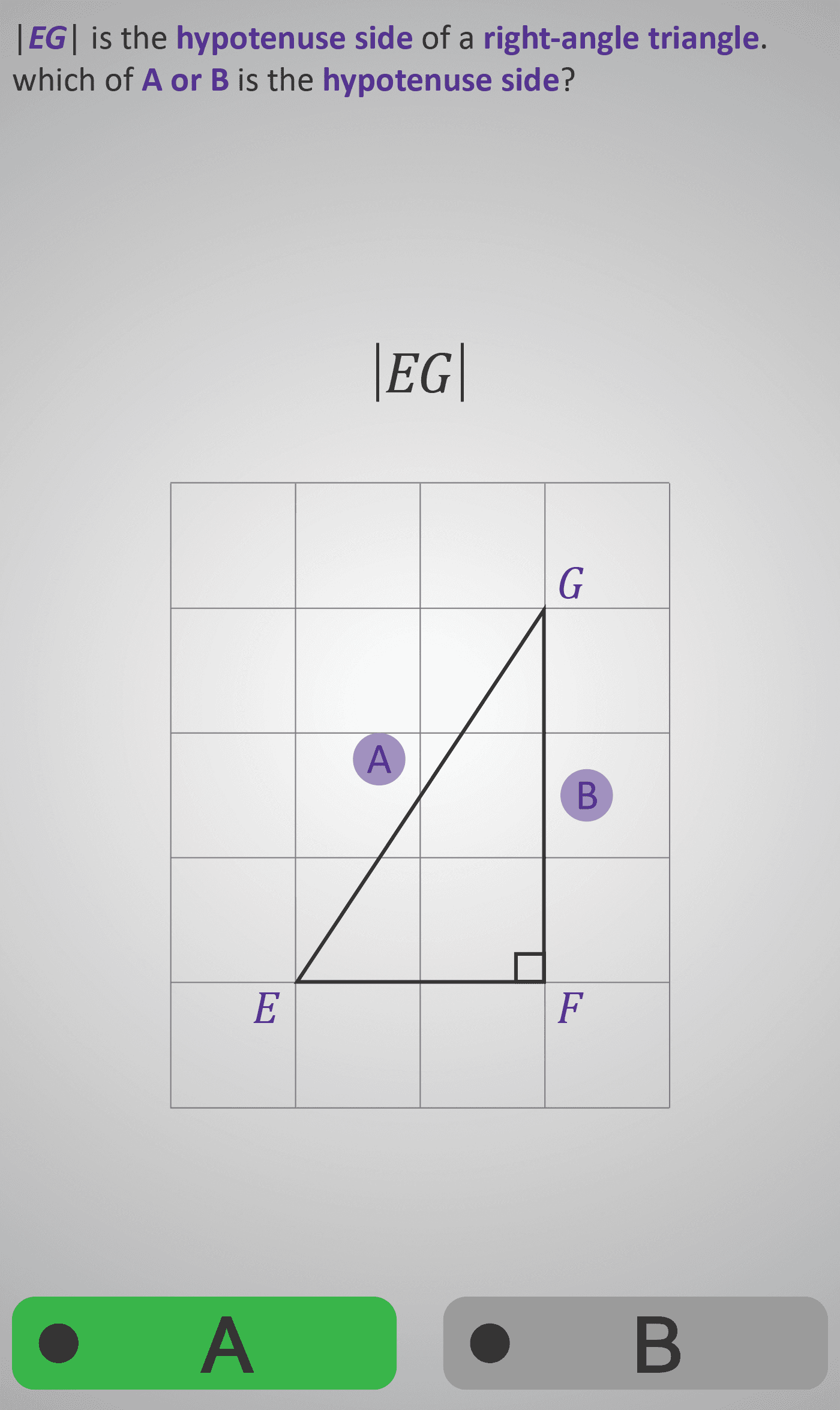
This Phlow develops students’ ability to calculate the distance between two points using Pythagoras’s theorem. Beginning with the right-angled triangle △EFG, learners identify the hypotenuse ∣EG∣ and the two shorter sides ∣EF∣ and ∣GF∣.
Through structured prompts, they substitute side lengths (2 and 3), square each, add them, and take the square root to find the diagonal length. By connecting each algebraic step — from |EG|² = 2² + 3² to |EG| = √13 ≈ 3.6 — students see how geometric reasoning becomes a concrete calculation process.
This Phlow bridges visual reasoning and procedural fluency, showing how squared relationships model distance. It builds accuracy with squaring, square roots, and calculator verification, preparing learners for the full coordinate distance formula in later levels.
Prerequisite Knowledge Required
- Right Triangles 2B – Identifying the hypotenuse.
- Pythagoras 2A – Understanding squares and square roots.
- Co-ordinate 3A – Applying Pythagoras on a grid.
- Understanding right-angled triangles and their sides.
- Ability to square numbers and find square roots accurately.
- Recognising horizontal and vertical distances on a grid.
Main Category
Geometry & Coordinate Algebra
Estimated Completion Time
Approx. 8–12 seconds per question (30 questions total). Total Time: 4–6 minutes.
Cognitive Load / Step Size
Moderate — the Phlow scaffolds each step of the process: identify sides → substitute values → square → add → square root. Visual cues and formula rewrites manage working memory effectively, supporting mastery of this multi-step concept.
Language & Literacy Demand
Moderate — core mathematical terms (hypotenuse, squared, square root, length) are repeated and highlighted. Diagrams and symbols carry meaning, reducing dependence on text for comprehension and enabling accessibility.
Clarity & Design
- Consistent triangle diagram anchors understanding across screens.
- Step-by-step handwritten animation mimics guided note-taking.
- Colour-coded cues separate geometric reasoning (shape) from computation (numbers).
- Calculator icon reinforces real-world accuracy checking.
Curriculum Alignment
Irish Junior Cycle Mathematics:
- Strand 3 – Geometry and Trigonometry
- Learning Outcomes:
- Apply Pythagoras’s theorem to calculate distances between points.
- Represent and reason with geometric relationships in the coordinate plane.
- Interpret and round numerical results appropriately.
Engagement & Motivation
Students move from recognising geometric structure to executing precise numerical steps. The clear link between geometry and algebra makes the concept purposeful and relevant to real-world tasks like measuring straight-line distance or design dimensions.
Error Opportunities & Misconceptions
- Adding before squaring (e.g., 2 + 3²).
- Forgetting to take the square root after summing squares.
- Squaring only one side or misordering operations.
- Mistaking the hypotenuse for a shorter side.
Each misconception is directly addressed through step sequencing and visual correction prompts (e.g., highlight changes colour after each correct transformation).
Transferability / Real-World Anchoring
High — understanding distance between points connects to navigation, architecture, physics, and computer graphics. The reasoning forms a cornerstone for later algebraic generalisation of the coordinate distance formula.
Conceptual vs Procedural Balance
Balanced — learners build procedural fluency through repeated practice, but every step is anchored in conceptual understanding of why distance equals the square root of the sum of squares. Visual–symbolic transitions reinforce both reasoning and method.
Learning Objectives Addressed
- Identify and label the hypotenuse in a right-angled triangle.
- Apply Pythagoras’s theorem to find the distance between two points.
- Square, add, and take square roots accurately to one decimal place.
- Understand how geometric reasoning becomes the coordinate distance formula.
What Your Score Says About You
- Less than 5: You may be mixing up the step order — review the square → add → root sequence.
- 6–7: You understand the method but may need to refine calculation accuracy or rounding.
- 8–9: Great conceptual grasp — minor slips could be in computation or rounding.
- 10 / 10: Excellent! You can confidently apply Pythagoras’s theorem — ready for the full coordinate formula next.