Co-ordinate 3C
Overview
In this Phlow, learners discover how to calculate the midpoint between two points K(x₁, y₁) and L(x₂, y₂). They begin by recalling or selecting the correct formula:
M = ( (x₁ + x₂) / 2 , (y₁ + y₂) / 2 )
Learners then substitute given coordinates — for example, x₁ = 5, y₁ = 3, x₂ = 1, y₂ = 5 — and simplify each step:
x = (5 + 1) / 2 = 3, y = (3 + 5) / 2 = 4, so the midpoint is (3, 4).
Through grid-based visuals, students see that the midpoint is the average of the x-values and y-values of the endpoints. Each screen isolates a single operation — add, divide, then interpret — making the connection between algebraic manipulation and geometric position clear. By the end, learners understand both how and why the midpoint formula works.
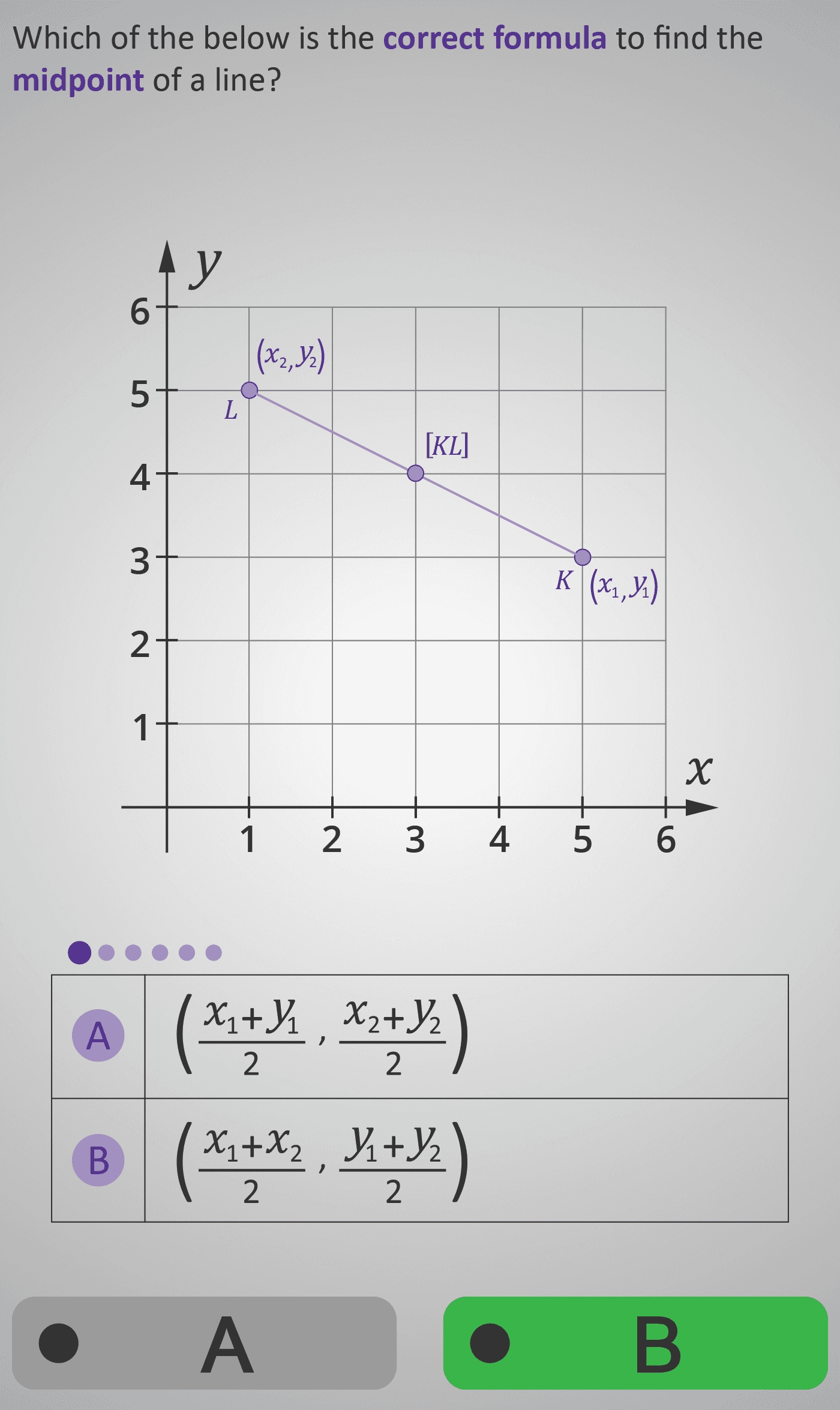
Prerequisite Knowledge Required
- Co-ordinate 3A – Reading points on a grid.
- Co-ordinate 3B – Using subscript notation (x₁, y₁, x₂, y₂).
- Recognising points and axes on a coordinate grid.
- Understanding addition and division operations.
- Knowing that subscripts identify two distinct points.
Main Category
Geometry & Coordinate Algebra
Estimated Completion Time
Approx. 8–12 seconds per question (30 questions total). Total Time: 4–6 minutes.
Cognitive Load / Step Size
Moderate — each question adds one new cognitive step: select the formula → substitute → add → divide → interpret. The linear sequence keeps processing demands low and supports retention through repetition and visual feedback.
Language & Literacy Demand
Medium — mathematical notation replaces long sentences, but key vocabulary (midpoint, fraction, simplify, coordinates) is consistently reinforced. Visual substitutions and grid diagrams help all learners follow reasoning without heavy reading.
Clarity & Design
- Step-by-step animation mirrors the order of operations (add → divide → plot).
- Purple highlights draw attention to each changing value.
- Grid diagrams show both algebraic and spatial perspectives.
- Handwriting motion reinforces procedural fluency through guided calculation.
Curriculum Alignment
Irish Junior Cycle Mathematics:
- Strand 3 – Geometry and Trigonometry
- Learning Outcomes:
- Use coordinates to determine geometric relationships.
- Apply formulae to find the midpoint between two points on the coordinate plane.
- Interpret midpoint results algebraically and graphically.
Engagement & Motivation
Students enjoy instant feedback as the midpoint appears on the line segment. The smooth transition from numerical averaging to visual confirmation creates a satisfying “aha” moment and reinforces mathematical meaning.
Error Opportunities & Misconceptions
- Mixing up x₁/y₁ and x₂/y₂ values.
- Forgetting to divide by 2 after adding.
- Thinking midpoint means “half the distance” rather than “average of coordinates.”
- Reversing coordinate order to (y, x).
Each error is pre-empted by visual feedback and explicit labelling of coordinates.
Transferability / Real-World Anchoring
High — midpoint calculation applies to maps, architecture, computer graphics, and engineering — wherever a central or halfway position is needed.
Conceptual vs Procedural Balance
Strong conceptual grounding with procedural reinforcement. Learners see why the formula averages both axes before they use it, ensuring deep understanding and confident application.
Learning Objectives Addressed
- Identify and use the midpoint formula correctly.
- Substitute numerical values into algebraic expressions.
- Simplify fractional results to whole numbers or decimals.
- Interpret the midpoint as the average location of two points.
What Your Score Says About You
- Less than 5: You may be mixing coordinate pairs or forgetting to divide by 2 — review the formula layout.
- 6–7: You grasp the concept but may make small arithmetic errors.
- 8–9: Strong procedural control — midpoints are accurate and well reasoned.
- 10 / 10: Excellent! You understand both how and why the midpoint formula works — ready for gradients next.