Co-ordinate 3D

Overview

This Phlow introduces students to the concept of gradient — a measure of how steep a line is on a coordinate grid. Starting with two points S(x₁, y₁) and T(x₂, y₂), learners use the gradient formula:

m = (y₂ - y₁) / (x₂ - x₁)

The Phlow breaks down the meaning of each part: the numerator (change in y) represents the rise, and the denominator (change in x) represents the run. Using coordinates such as (1, 3) and (6, 5), students substitute values, calculate each difference, and simplify:
m = (5 - 3) / (6 - 1) = 2 / 5 = 0.4

Visual cues show how each subtraction step corresponds to movement on the grid — up 2 units, across 5 units. By the end, students understand gradient as both a numerical ratio and a visual measure of steepness, preparing them for linear equations and rate of change problems.

Step 1 / 5

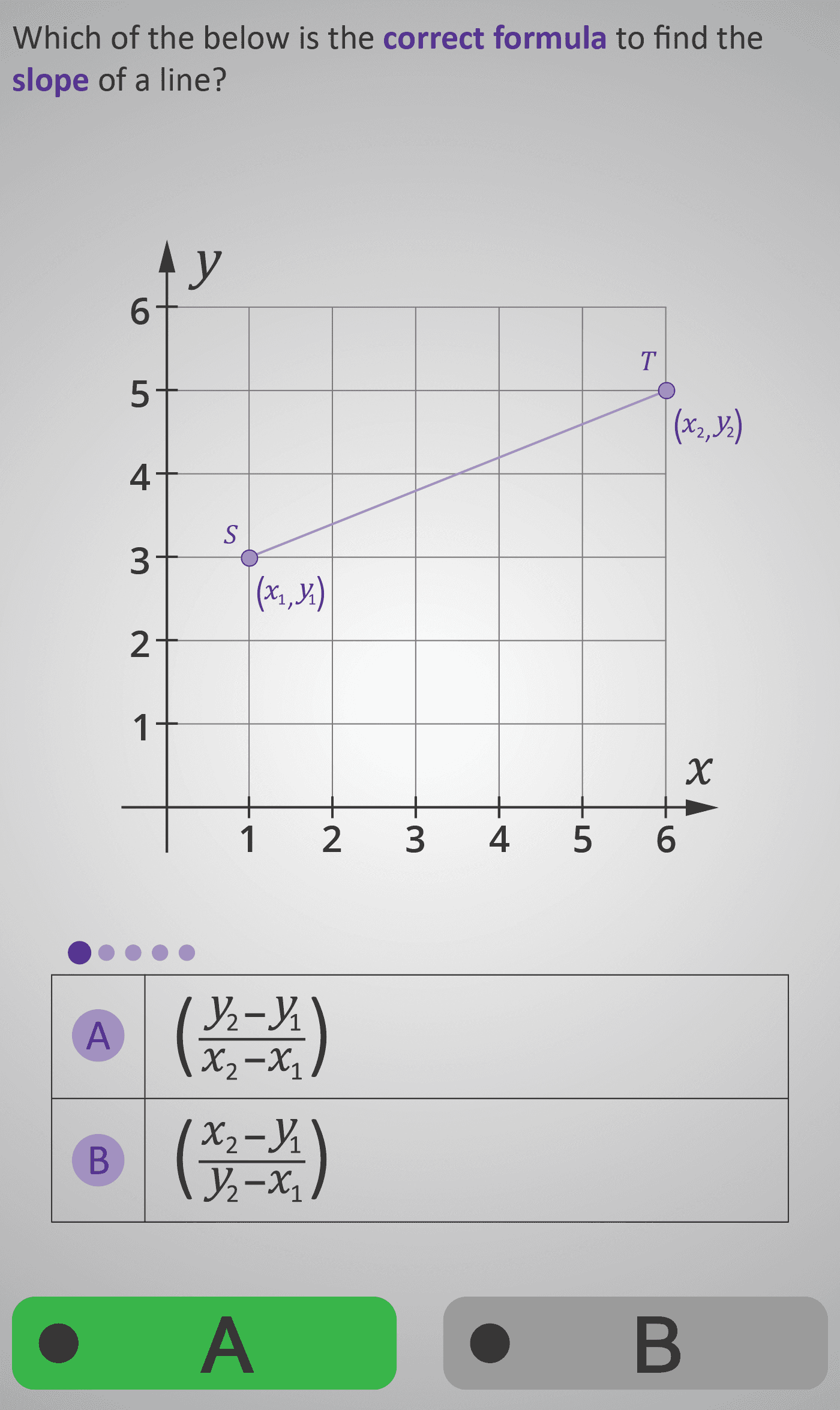
Prerequisite Knowledge Required

Co-ordinate 3B – Distance between two points.
Co-ordinate 3C – Midpoint of a line segment.
Understanding of coordinate pairs (x, y) and grid plotting.
Ability to subtract one number from another accurately.
Familiarity with the concepts of horizontal and vertical change.
Basic fraction simplification skills.

Main Category

Geometry & Coordinate Algebra

Estimated Completion Time

Approx. 8–12 seconds per question (30 questions total). Total Time: 4–6 minutes.

Cognitive Load / Step Size

Moderate — each question focuses on one key action: identify the formula → substitute → find each difference → divide → interpret. Visual annotations and incremental reveals reduce abstraction while maintaining progression toward full procedural fluency.

Language & Literacy Demand

Moderate — key mathematical terms (slope, gradient, rise, run) are reinforced through consistent colour highlights and visual context. Symbolic reasoning outweighs text-heavy explanation, supporting diverse literacy levels.

Clarity & Design

Simple, single-line graph with labelled points (S and T).
Table of coordinates displayed beside the graph for substitution clarity.
Handwritten-style progression mirrors note-taking and aids retention.
Formula steps and visual arrows link algebraic operations to geometric movement.

Curriculum Alignment

Irish Junior Cycle Mathematics:

Strand 3 – Geometry and Trigonometry
Learning Outcomes:

Interpret and calculate the slope of a line using coordinates.
Understand gradient as a rate of change between two variables.
Connect slope to proportional reasoning and linear relationships.

Engagement & Motivation

The Phlow provides instant visual feedback as the slope is calculated and shown on the grid. Learners experience the satisfaction of seeing their numerical result (e.g. m = 0.4) align perfectly with the steepness of the line, linking abstract calculation to intuitive understanding.

Error Opportunities & Misconceptions

Reversing the order of subtraction (y₁ - y₂ instead of y₂ - y₁).
Using x-values in the numerator or y-values in the denominator.
Forgetting to simplify the fraction or misinterpreting negative gradients.
Assuming gradient only applies to upward-sloping lines.

Each common error is addressed visually through guided correction and direction arrows that clarify rise/run orientation.

Transferability / Real-World Anchoring

High — understanding gradient supports learning in linear equations, physics, engineering, and data analysis. It applies to real-world reasoning about ramps, speed-time graphs, and slopes in design or construction.

Conceptual vs Procedural Balance

Balanced — procedural fluency (substitute, subtract, divide) is tightly connected to conceptual understanding (rate of change). The Phlow blends visual geometry with numerical logic for lasting comprehension.

Learning Objectives Addressed

Identify and use the correct gradient formula for two points.
Substitute coordinate values accurately and simplify results.
Express gradients as fractions and decimals.
Interpret slope as vertical change divided by horizontal change.

What Your Score Says About You

Less than 5: You may be mixing coordinate order — review which values go in the numerator and denominator.
6–7: You understand the process but need to refine subtraction order and sign accuracy.
8–9: Strong procedural mastery — gradients are mostly correct and well simplified.
10 / 10: Excellent! You can calculate and interpret gradients confidently — ready for equations of lines next.