Co-ordinate 3H
Overview
In this Phlow, students practise converting coordinates of two plotted points — K and L — into standard algebraic form using subscripts:
K(x₁, y₁) and L(x₂, y₂)
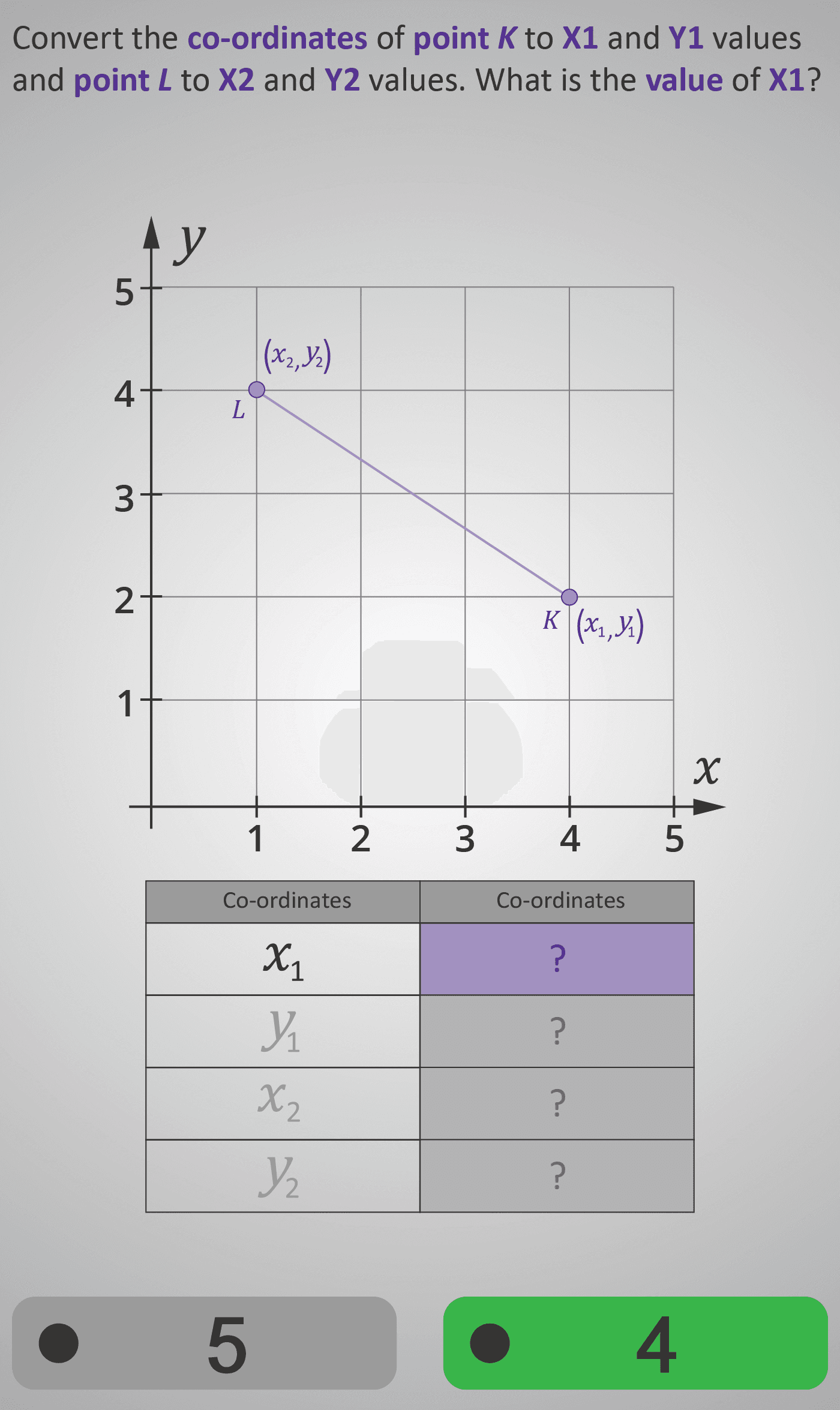
Learners begin by identifying the coordinates of each point on the grid, first finding x₁, then y₁, followed by x₂ and y₂. For example, if point K is at (4, 2) and point L is at (1, 4), students record:
x₁ = 4, y₁ = 2, x₂ = 1, y₂ = 4
This process helps students understand that each subscript refers to a specific point, enabling clear differentiation between two positions on the same grid. Through scaffolded questioning, learners isolate one variable at a time, developing fluency in identifying and recording ordered pairs systematically.
By the end of the Phlow, students can confidently translate geometric points into algebraic notation — a crucial step before calculating distance, midpoint, and gradient in higher-level Phlows.
Prerequisite Knowledge Required
- Co-ordinate 3E – Calculating area from grid dimensions.
- Co-ordinate 3F – Plotting points accurately.
- Co-ordinate 3G – Identifying x- and y-coordinates of a point.
- Understanding that coordinates are written as ordered pairs (x, y).
- Ability to locate and interpret points on a coordinate grid.
- Counting confidently along both axes from the origin.
Main Category
Geometry & Coordinate Algebra
Estimated Completion Time
Approx. 8–12 seconds per question (30 questions total). Total Time: 4–6 minutes.
Cognitive Load / Step Size
Moderate — students manage four labelled variables (x₁, y₁, x₂, y₂) while recalling coordinate order. Visual cues, colour coding, and sequential prompts minimise working-memory strain and support accuracy.
Language & Literacy Demand
Medium — introduces symbolic notation with subscripts. Consistent phrasing, side-by-side visuals, and explicit alignment between table values and grid points ensure comprehension.
Clarity & Design
- Colour-coded coordinates distinguish K from L for clarity.
- Subscript notation displayed beside each point reinforces structure.
- Clear axis labelling and spacing prevent confusion.
- Stepwise visual build links each coordinate to its symbolic representation.
Curriculum Alignment
Irish Junior Cycle Mathematics:
- Strand 3 – Geometry and Trigonometry
- Learning Outcomes:
- Record the coordinates of two points on the coordinate plane.
- Understand and apply subscript notation for coordinate pairs.
- Prepare for distance, midpoint, and gradient formulas.
Engagement & Motivation
The “fill-in-the-table” format provides a tangible sense of progress. Learners experience growing confidence as each coordinate is revealed and recorded, hinting at its role in upcoming algebraic formulas.
Error Opportunities & Misconceptions
- Swapping K and L (subscripts reversed).
- Mixing x- and y-values within a pair.
- Forgetting that x comes before y.
- Mis-ordering x₁, x₂ or y₁, y₂ in tabulated form.
Visual differentiation (colour, labels, alignment) addresses these directly, reinforcing accuracy and symbolic understanding.
Transferability / Real-World Anchoring
High — subscript notation is universal in physics, computer graphics, engineering, and navigation. Recognising x₁, y₁, x₂, y₂ establishes algebraic readiness for line, vector, and transformation work.
Conceptual vs Procedural Balance
Balanced — learners apply a clear procedure (identify → record → label) while developing conceptual awareness that notation encodes relationships between two distinct points.
Learning Objectives Addressed
- Identify and label coordinates using subscript notation.
- Distinguish between two points on the coordinate plane.
- Connect visual points to symbolic algebraic representation.
- Lay the groundwork for distance, midpoint, and gradient formulas.
What Your Score Says About You
- Less than 5: You may be mixing up K and L — review which is x₁, y₁ and which is x₂, y₂.
- 6–7: You understand coordinate order but should double-check axis direction and subscripts.
- 8–9: Excellent understanding — you can match and label coordinates confidently.
- 10 / 10: Superb! You’re ready to calculate gradients, midpoints, and distances between two points.