Fraction 3B
Overview
In this Phlow, learners are introduced to adding fractions with unlike denominators. They begin with the example ½ + ⅔ and are guided through the reasoning step-by-step:
- Find a common denominator: The system asks, “What is the number below the line that 2 and 3 divide into evenly?” Students identify 6 as the lowest common multiple.
- Convert each fraction: The Phlow shows how ½ becomes 3⁄6 and ⅔ becomes 4⁄6, reinforcing that multiplying both numerator and denominator by the same number keeps the fraction’s value the same.
- Add the numerators: Finally, learners calculate 3 + 4 = 7, giving the total 7⁄6.
The process emphasises that denominators must match before adding and that only the numerators are combined. Clear colour coding — purple numerators, grey boxes, and green feedback — helps learners track each step visually.
By the end, students understand why fractions must have the same denominator before addition — a key conceptual bridge between multiplication, division, and proportional reasoning.
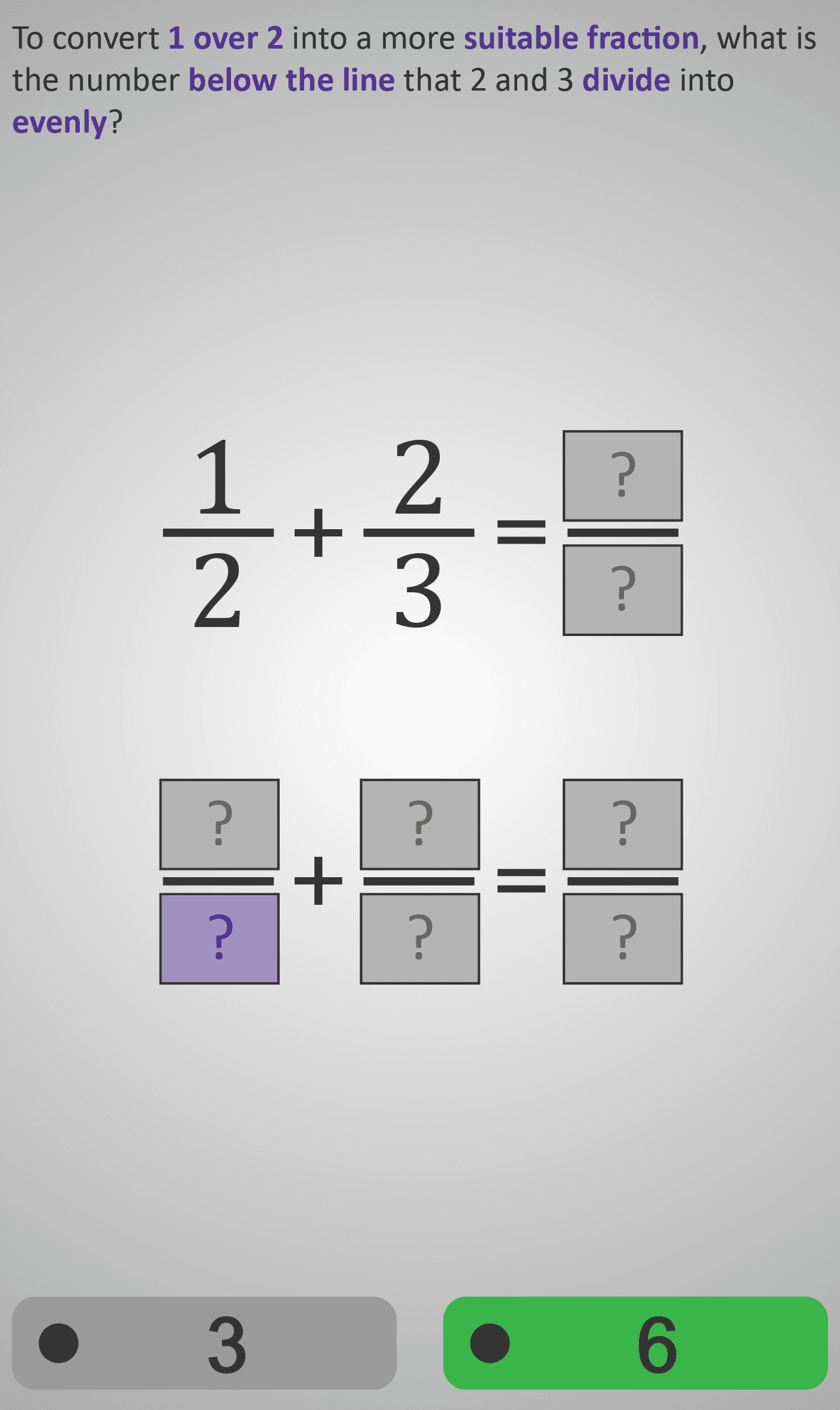
Prerequisite Knowledge Required
- Fraction 3A – Finding the Lowest Common Multiple.
- Multiply 2B – Equivalent Fractions.
- Divide 2A – Simple Division Facts.
- Understanding that multiplying numerator and denominator by the same number creates an equivalent fraction.
- Familiarity with multiples and finding common denominators.
- Confidence adding fractions with the same denominator.
- Awareness of improper fractions (numerator > denominator).
Main Category
Fractions / Operations with Fractions
Estimated Completion Time
Approx. 8–10 seconds per step (6 steps total). Total Time: 2–3 minutes.
Cognitive Load / Step Size
Moderate — the Phlow breaks a multi-step procedure (LCM → conversion → addition) into small, manageable actions. Each step builds logically on the previous one, supported by strong visuals and minimal text to reduce strain on working memory.
Language & Literacy Demand
Low to Moderate — repeated phrasing such as “What is the number below the line…” and “What over 6 equals…” builds mathematical language naturally. The vocabulary (below the line, divide evenly, add to) strengthens understanding through consistent use.
Clarity & Design
- Large, clean fraction visuals for easy reading.
- Consistent placement of purple highlights draws attention to active numerators.
- Step-by-step transitions prevent overload and guide reasoning visually.
- Yes/No format ensures focus on understanding rather than memorisation.
Curriculum Alignment
Irish Junior Cycle Mathematics:
- Strand 1 – Number
- Substrand – Fractions and Operations
- Learning Outcomes:
- Add fractions with different denominators by finding the lowest common multiple.
- Convert between equivalent fractions to create common denominators.
- Understand that denominators remain constant during addition.
Engagement & Motivation
High — students experience satisfaction as the fractions visually align step-by-step. Each correct input provides immediate feedback (✓ / ✗), building mastery through active interaction and success reinforcement.
Error Opportunities & Misconceptions
- Adding denominators instead of keeping them the same.
- Forgetting to convert both fractions to the same denominator.
- Confusing Lowest Common Multiple with Highest Common Factor.
- Treating ½ + ⅔ as ³⁄₅.
The Phlow prevents these by scaffolding denominator alignment before addition, ensuring conceptual understanding before procedural execution.
Transferability / Real-World Anchoring
High — adding fractions underpins reasoning in ratio, proportion, measurement, algebraic fractions, and everyday problem-solving (e.g., recipes, probabilities, distances). Mastery here supports flexible thinking across multiple domains.
Conceptual vs Procedural Balance
Balanced — learners apply a step-by-step procedure while understanding why each step matters. Conceptual understanding of common denominators is continually reinforced through visual alignment and verbal cues.
Learning Objectives Addressed
- Identify and apply the lowest common denominator when adding fractions.
- Convert fractions to equivalent forms with equal denominators.
- Add numerators while keeping the denominator constant.
- Explain why ½ + ⅔ = ⁷⁄₆.
What Your Score Says About You
- Less than 5: You may be adding denominators or skipping the conversion step — review how to make fractions equivalent before adding.
- 6–7: You understand the process but may need more practice finding the lowest common denominator.
- 8–9: You’re confidently applying the correct steps — excellent progress!
- 10 / 10: Outstanding! You can add fractions with different denominators — ready to simplify and work with mixed numbers next.