Probability 3C

Overview

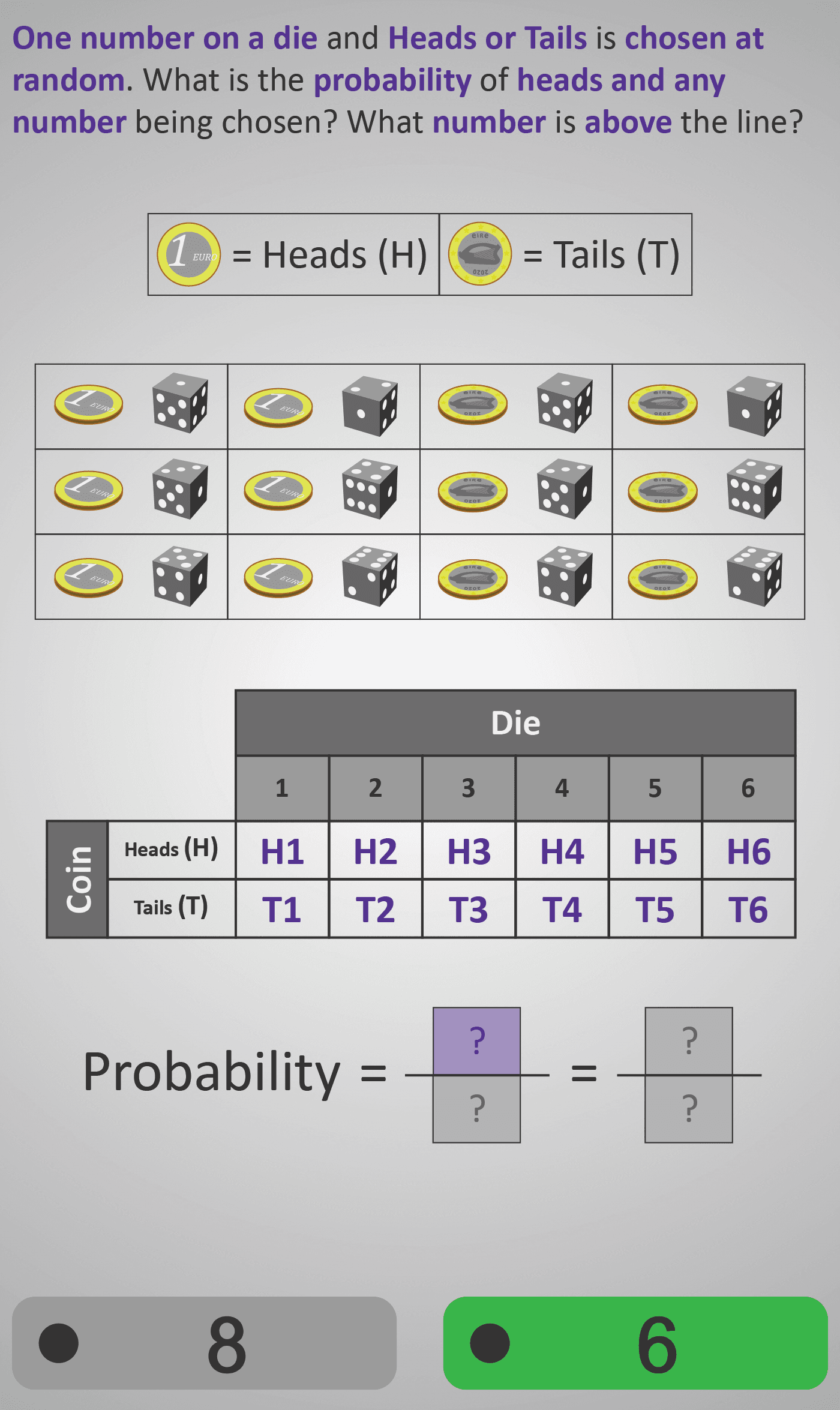
In this Phlow, learners build on their understanding of simple probability by exploring combined events — in this case, flipping a coin and rolling a six-sided die. They are introduced to a visual sample space showing all 12 possible outcomes (H1–H6, T1–T6), connecting concrete images (coins and dice) to symbolic probability notation.

Students are guided through a clear, step-by-step process:

Understanding total outcomes: 2 for the coin × 6 for the die = 12 total.
Identifying favourable outcomes: e.g., all results showing Heads (6 total).
Writing the probability: favourable over total → 6/12.
Simplifying the fraction: e.g., 6/12 = 1/2.

Each screen isolates one skill — finding the numerator, denominator, or simplifying — before combining them. Visual counting and numerical reasoning work together to strengthen understanding of how probability connects to fractions.

The activity reinforces the rule: Probability = Number of favourable outcomes ÷ Total possible outcomes, while linking to prior fraction work. This integration prepares students for more abstract probability calculations using spinners, tables, and tree diagrams in later levels.

Step 1 / 4

Prerequisite Knowledge Required

Understanding of basic probability from single events.
Knowledge of fractions and simplifying to simplest form.
Recognition that probability = favourable ÷ total outcomes.
Completion of Probability 3A (fractions) and 3B (complements).

Main Category

Data & Probability / Probability from Combined Events

Estimated Completion Time

Approx. 7 minutes (four progressive visual + symbolic tasks).

Cognitive Load / Step Size

Moderate — combines multiple previously learned ideas (fractions, counting, simplification) but supports learners through clear grids and consistent phrasing. Each screen introduces one new layer at a time.

Language & Literacy Demand

Low to Moderate — key terms like favourable, simplest form, and numerator/denominator are repeated and paired with visuals. Purple highlights and labelled grids help decode meaning without heavy text reliance.

Clarity & Design

Grid of outcomes (coin × die) shows all 12 possibilities clearly.
Symbolic table (H1–T6) reinforces systematic thinking.
Purple highlighting connects questions to fraction structure.
Alternating conceptual (visual) and procedural (simplification) tasks maintain flow.

Curriculum Alignment

Irish Junior Cycle Mathematics – Learning Outcome 1.11

Identify all possible outcomes of two combined random events.
Calculate probabilities using sample spaces.
Simplify probability fractions to simplest form.

Engagement & Motivation

High — the use of coins and dice connects mathematics to familiar, game-like contexts. Moving from pictures to tables to fractions provides a tangible and rewarding sense of progress.

Error Opportunities & Misconceptions

Forgetting that there are 12 total outcomes (2 × 6).
Inverting the fraction (total ÷ favourable).
Errors in simplifying fractions.

Each misconception is isolated and addressed with feedback, examples, and colour cues.

Transferability / Real-World Anchoring

Strong — learners connect to everyday random processes like games, experiments, or fair draws. The concepts apply directly to reasoning about fairness, odds, and sample modelling in real-world data.

Conceptual vs Procedural Balance

Conceptual: understanding how events combine to form all outcomes.
Procedural: writing, simplifying, and reasoning with probability fractions.

Learning Objectives Addressed

List and interpret outcomes of combined random events.
Calculate probability fractions from total and favourable outcomes.
Simplify probabilities accurately to their simplest form.
Link visual reasoning to formal probability notation.

What Your Score Says About You

Below 4: Review how to count total outcomes — check each combination (H1–T6).
5–7: You understand combined events — practise simplifying fractions correctly.
8–9: Excellent progress — you can interpret and simplify probabilities with confidence.
10 / 10: Perfect! You’ve mastered probability fractions — ready for Probability 3D, where you’ll apply these ideas to fairness and real-world comparisons.