Pythagoras’ Theorem 3
Overview
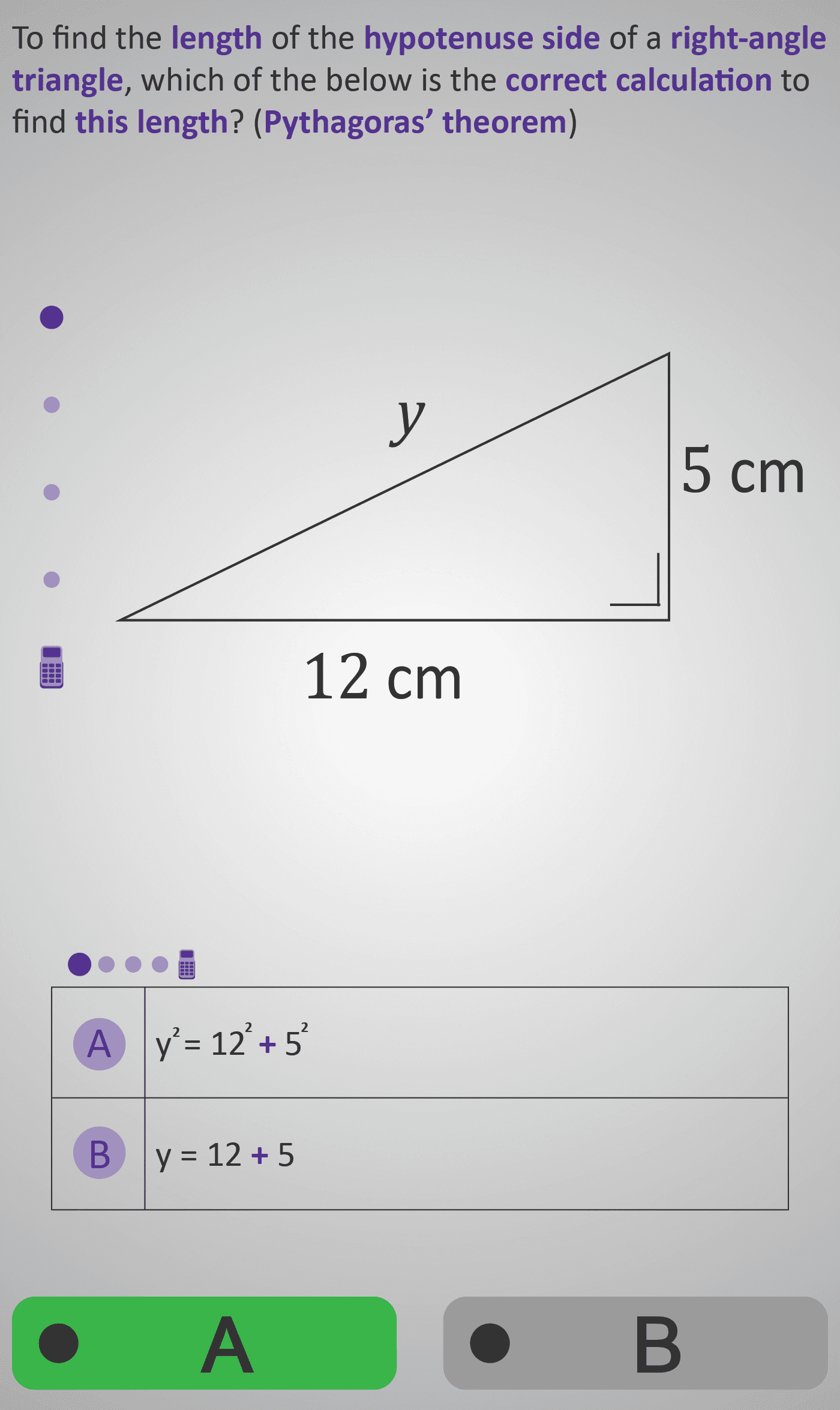
In this Phlow, students move from understanding Pythagoras’ theorem conceptually to executing it systematically. They are shown a right-angled triangle with perpendicular sides of 5 cm and 12 cm, and a hypotenuse labelled y.
The learner progresses through five guided steps:
- Identify the correct formula for the hypotenuse: y² = 12² + 5²
- Substitute and simplify each squared value: y² = 144 + 25
- Add the squares to find y² = 169
- Take the square root to isolate y: y = √169
- Find the final length using a calculator: y = 13 cm
Each stage reinforces mathematical reasoning — from formula to computation. The use of handwritten working animations and multiple-choice checks helps learners internalise both the logic and the sequence of Pythagoras’ theorem.
By the end of this Phlow, students can:
- Identify the hypotenuse in a right-angled triangle.
- Apply Pythagoras’ theorem correctly and confidently.
- Substitute values and carry out calculations accurately.
- Express their final answer with appropriate units.
This Phlow bridges visual comprehension and procedural fluency, preparing learners for applying Pythagoras’ theorem in real-world geometry and measurement problems.
Prerequisite Knowledge Required
- Understanding that the hypotenuse is the longest side opposite the right angle.
- Familiarity with squaring and square roots (from Number and Algebra Phlows).
- Knowledge of right-angled triangles and identifying perpendicular sides.
- Basic calculator use for arithmetic and square root operations.
Main Category
Geometry & Measurement / Right-Angled Triangles
Estimated Completion Time
Approx. 7–8 minutes (five guided calculation steps).
Cognitive Load / Step Size
Low to Moderate — the process is scaffolded line by line with visual cues and minimal new information per screen. This reduces cognitive strain and encourages sequential reasoning and procedural fluency.
Language & Literacy Demand
Moderate — key mathematical terms like “hypotenuse”, “square”, and “square root” are colour-highlighted for clarity. Visuals of handwritten working reinforce understanding of symbolic notation and algebraic structure.
Clarity & Design
- Each step builds directly from the previous one, ensuring logical flow.
- Consistent layout (triangle on right, working on left) enhances focus.
- Purple highlights link operations (e.g., add, square root) to visual steps.
- The gradual reveal mirrors a teacher’s live explanation on a whiteboard.
Curriculum Alignment
Irish Junior Cycle Mathematics – Learning Outcome 3.5
- Apply Pythagoras’ theorem to calculate the length of a side in a right-angled triangle.
- Use squares and square roots in numerical contexts.
- Justify results through substitution and accurate reasoning.
Engagement & Motivation
High — the interactive step-by-step method transforms abstract algebra into visual, hands-on reasoning. Each step feels rewarding, with clear feedback reinforcing success and building mastery.
Error Opportunities & Misconceptions
- Adding side lengths directly instead of squaring them.
- Forgetting to take the square root at the end.
- Confusing which side is the hypotenuse.
These are pre-empted with explicit guided corrections and step-by-step prompts.
Transferability / Real-World Anchoring
Strong — this method mirrors real-world geometry reasoning, such as finding ladder lengths, ramp angles, and navigation distances. It gives mathematical principles immediate practical value.
Conceptual vs Procedural Balance
Conceptual: understanding how Pythagoras’ theorem links side lengths in right-angled triangles.
Procedural: executing calculations and substitutions accurately, step by step.
Learning Objectives Addressed
- Recognise and label sides of a right-angled triangle.
- Apply Pythagoras’ theorem to find the hypotenuse.
- Evaluate and simplify expressions involving squares and roots.
- Present answers clearly with correct units.
What Your Score Says About You
- Less than 15: Review the steps — ensure sides are squared before adding.
- 16–22: You understand the method — practise combining and simplifying accurately.
- 23–29: Strong grasp — you can apply Pythagoras’ theorem confidently and correctly.
- 30 / 30: Excellent! You’ve mastered the process — ready for Pythagoras’ Theorem 4, where you’ll find missing shorter sides and apply the theorem to word problems.