Venn Diagram 3A
Overview
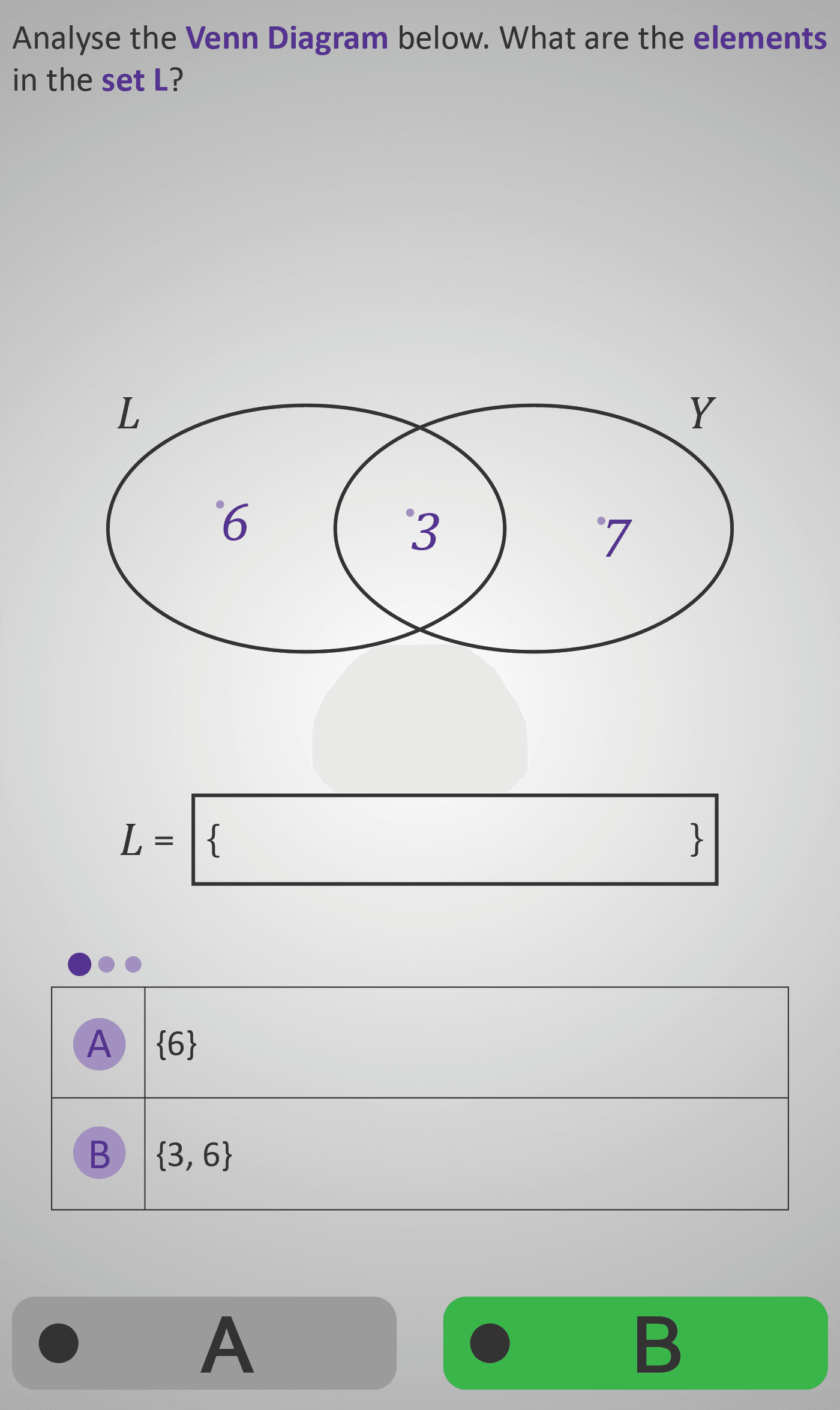
In this Phlow, learners are introduced to the fundamentals of set notation through visual exploration of Venn Diagrams. Two overlapping circles labelled L and Y illustrate how numbers can belong to one set, both sets, or neither. Students begin by identifying elements unique to each set before recognising those shared by both (the intersection).
As they progress, learners identify the union of sets (L ∪ Y) — the collection of all elements within both circles — and record these using proper mathematical notation, e.g. L = {3, 6}. This structured visual approach builds a clear bridge between concrete visual grouping and abstract algebraic representation.
Through repeated interaction with overlapping diagrams, learners develop logical reasoning, set vocabulary, and confidence using curly bracket notation. This Phlow provides a solid foundation for later work in data handling, probability, and algebraic logic.
- Identify elements belonging to specific sets in a Venn Diagram.
- Recognise intersections (shared elements) and unions (combined elements).
- Write sets correctly using curly bracket notation.
- Use logical reasoning to determine set membership from diagrams.
Prerequisite Knowledge Required
- Awareness that sets group related elements together.
- Understanding of basic number representation and counting.
- Familiarity with curly bracket notation (e.g. {a, b, c}).
- Recognition of overlapping areas representing shared membership.
- Linked earlier Phlows: Sort 2A – Classifying Objects and Numbers; Group 2B – Recognising Shared Features; Symbol 2C – Using Mathematical Notation.
Main Category
Data and Probability → Sets and Venn Diagrams
Estimated Completion Time
Approx 6–10 seconds per question (30 total). Total time: 3–5 minutes.
Learning Outcomes
- Identify which elements belong to individual sets.
- Recognise intersections (L ∩ Y) and unions (L ∪ Y).
- Represent sets accurately using curly bracket notation.
- Use diagrams to reason about set membership and relationships.
Cognitive Load / Step Size
Low to moderate — learners move from identifying one set to understanding overlap and union. The limited number of elements per diagram ensures focus on core reasoning, while repetition across similar layouts supports conceptual reinforcement.
Language & Literacy Demand
Low — mathematical terms such as set, element, union, and intersection are introduced gradually and reinforced visually. Consistent phrasing (“elements in set L”, “in both sets”) aids comprehension and memory.
Clarity & Design
- Clean, uncluttered layout with clear circle overlaps.
- Numbers spaced evenly to indicate membership regions.
- Purple highlights focus attention on current question area.
- Notation examples ({...}) displayed beside visuals for reinforcement.
Curriculum Alignment
Strand: Data and Probability → Sets and Number Relationships
Learning Outcome: Represent and describe relationships between sets using diagrams and notation, including union and intersection.
(Aligned with Junior Cycle Mathematics – Strand 1: Number and Relationships, Learning Outcomes 1.14 & 1.15.)
Engagement & Motivation
The interactive, puzzle-like nature of set reasoning keeps students engaged. Discovering which numbers “belong where” promotes curiosity and builds a satisfying sense of mastery in an early algebraic context.
Error Opportunities & Misconceptions
- Confusing union (L ∪ Y) with intersection (L ∩ Y).
- Omitting shared elements from both sets.
- Incorrect use of curly brackets or missing commas.
Immediate feedback, repeated structure, and visual emphasis on overlaps help address these misconceptions effectively.
Transferability / Real-World Anchoring
Understanding sets underpins skills in data organisation, probability, and logic-based reasoning across mathematics, science, and computer studies. It enhances analytical thinking and systematic classification in both academic and everyday contexts.
Conceptual vs Procedural Balance
Conceptual: Understanding why elements belong to specific regions of a Venn Diagram.
Procedural: Writing correct set notation for unions and intersections.
The Phlow integrates both to create lasting conceptual clarity and procedural fluency.
What Your Score Says About You
- Below 15: Review how to identify overlapping regions and shared elements.
- 16–22: Growing confidence in interpreting Venn Diagrams and writing sets.
- 23–29: Excellent understanding — refine notation precision and consistency.
- 30 / 30: Mastery — confidently analyses Venn Diagrams and expresses sets accurately in notation.