Venn Diagram 3C
Overview
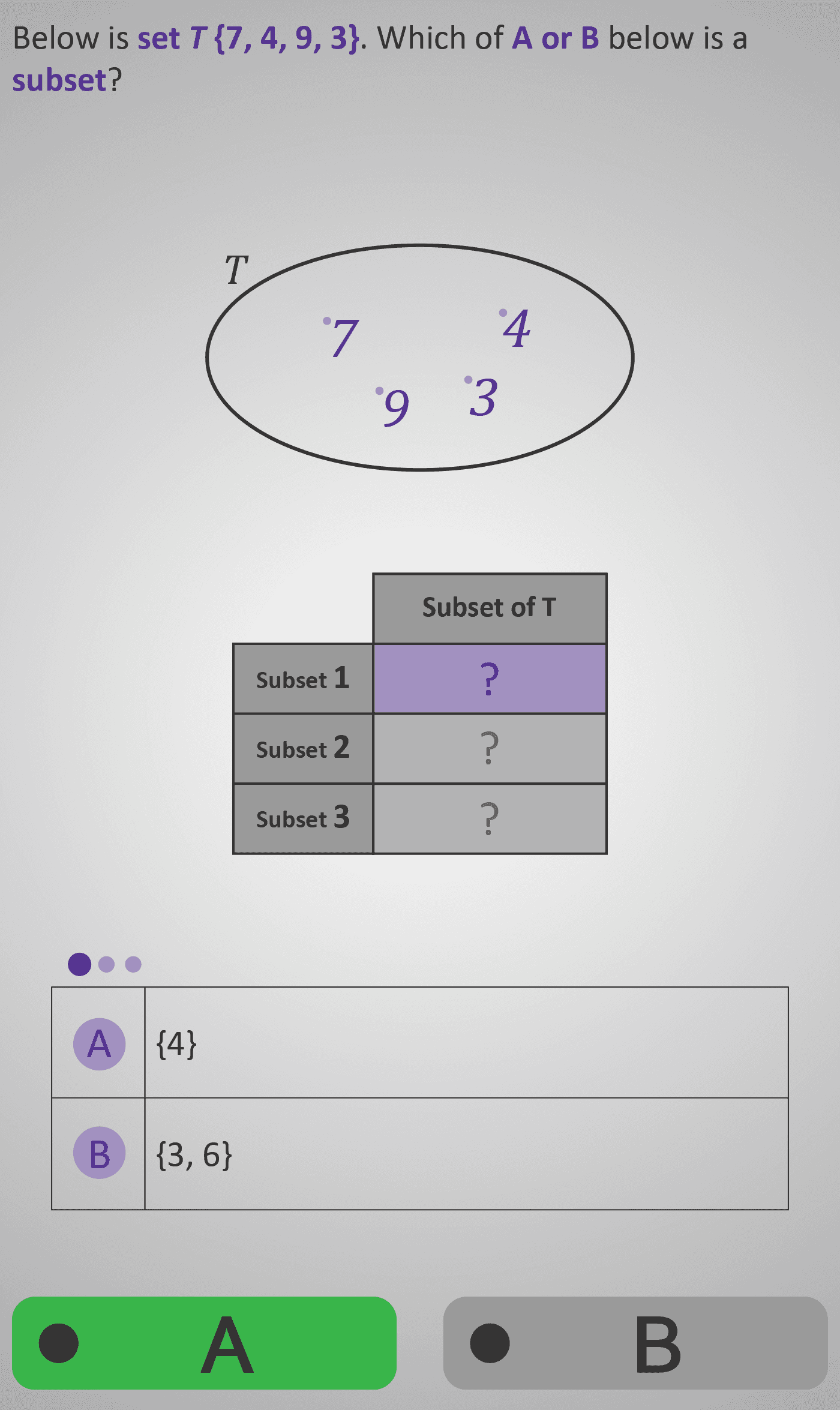
In this Phlow, learners advance their understanding of set theory by exploring the concept of subsets — smaller sets whose elements all belong to a larger “parent” set. Using a clear visual model (e.g., T = {7, 4, 9, 3}), students examine whether smaller groups such as {4}, {3, 7}, or {3, 4, 7} qualify as subsets of T.
Through guided comparisons, learners test inclusion rules logically: every element of a subset must already exist within the parent set, and no new or foreign elements can be introduced. By practising with multiple examples, students strengthen reasoning about inclusion, membership, and notation.
This Phlow transforms abstract ideas into visual logic, developing foundational skills for advanced topics like probability, algebraic logic, and data classification. Learners move from identifying single sets to understanding how sets relate and nest within one another.
- Determine whether one set is a subset of another.
- Recognise that all subset elements must already belong to the parent set.
- Use curly bracket notation correctly when describing subsets.
- Develop logical reasoning about inclusion and exclusion within sets.
Prerequisite Knowledge Required
- Ability to identify elements within a set.
- Understanding of curly bracket notation for sets (e.g. {1, 2, 3}).
- Basic concept of inclusion — one group being part of another.
- Experience comparing two groups visually or numerically.
- Linked earlier Phlows: Venn Diagram 3A – Identifying Elements in Sets; Venn Diagram 3B – Interpreting Overlaps; Sort 2A – Classifying by Shared Properties.
Main Category
Data and Probability → Sets and Subsets
Estimated Completion Time
Approx 8–12 seconds per question (30 total). Total time: 4–6 minutes.
Learning Outcomes
- Identify whether a given set is a subset of another.
- Recognise that all subset elements must exist within the parent set.
- Apply set notation correctly to describe subset relationships.
- Reason logically about inclusion and exclusion in set relationships.
Cognitive Load / Step Size
Moderate — this Phlow moves from recognition to reasoning. Students must now evaluate relationships between sets rather than just reading elements, requiring a higher level of abstraction. Repetition and visual scaffolding regulate cognitive effort for smooth progression.
Language & Literacy Demand
Medium — terms such as subset, element, and inclusion are introduced in context and repeated across examples. Consistent phrasing like “Which of A or B is a subset?” supports comprehension through predictability and pattern recognition.
Clarity & Design
- Clean single-oval diagram showing the parent set.
- Tabular presentation of possible subsets enhances structure and focus.
- Use of purple highlighting to emphasise valid subset relationships.
- Minimal clutter ensures attention remains on logical reasoning.
Curriculum Alignment
Strand: Data and Probability → Sets and Logic
Learning Outcome: Describe relationships between sets, identify subsets, and use formal notation to represent inclusion.
(Aligned with Junior Cycle Mathematics – Strand 1: Number and Relationships, Learning Outcomes 1.14 & 1.15.)
Engagement & Motivation
The step-by-step “logic puzzle” format is engaging and accessible. Each example provides immediate confirmation of understanding, creating a rewarding flow that reinforces curiosity and logical confidence.
Error Opportunities & Misconceptions
- Believing a subset must contain all elements of the parent set.
- Including numbers not present in the parent set.
- Confusing subset logic with intersection or union concepts.
Consistent feedback and visual checking (subset inside parent oval) correct these misconceptions early, reinforcing correct reasoning patterns.
Transferability / Real-World Anchoring
Subset reasoning underpins many real-world and academic applications — from data filtering and classification to probability, database logic, and computer programming. It nurtures analytical thinking essential for mathematics and digital literacy.
Conceptual vs Procedural Balance
Conceptual: Understanding how one set can exist within another.
Procedural: Checking and writing subsets correctly in notation.
Emphasis is on conceptual clarity, ensuring students understand inclusion rather than memorising rules.
What Your Score Says About You
- Below 15: Beginning to understand subset logic — practise checking membership carefully.
- 16–22: Developing good awareness of inclusion/exclusion rules.
- 23–29: Strong logical reasoning — confident in verifying subset relationships.
- 30 / 30: Mastery — fluent in recognising and expressing subset logic with accuracy and understanding.