Venn Diagram 3D
Overview
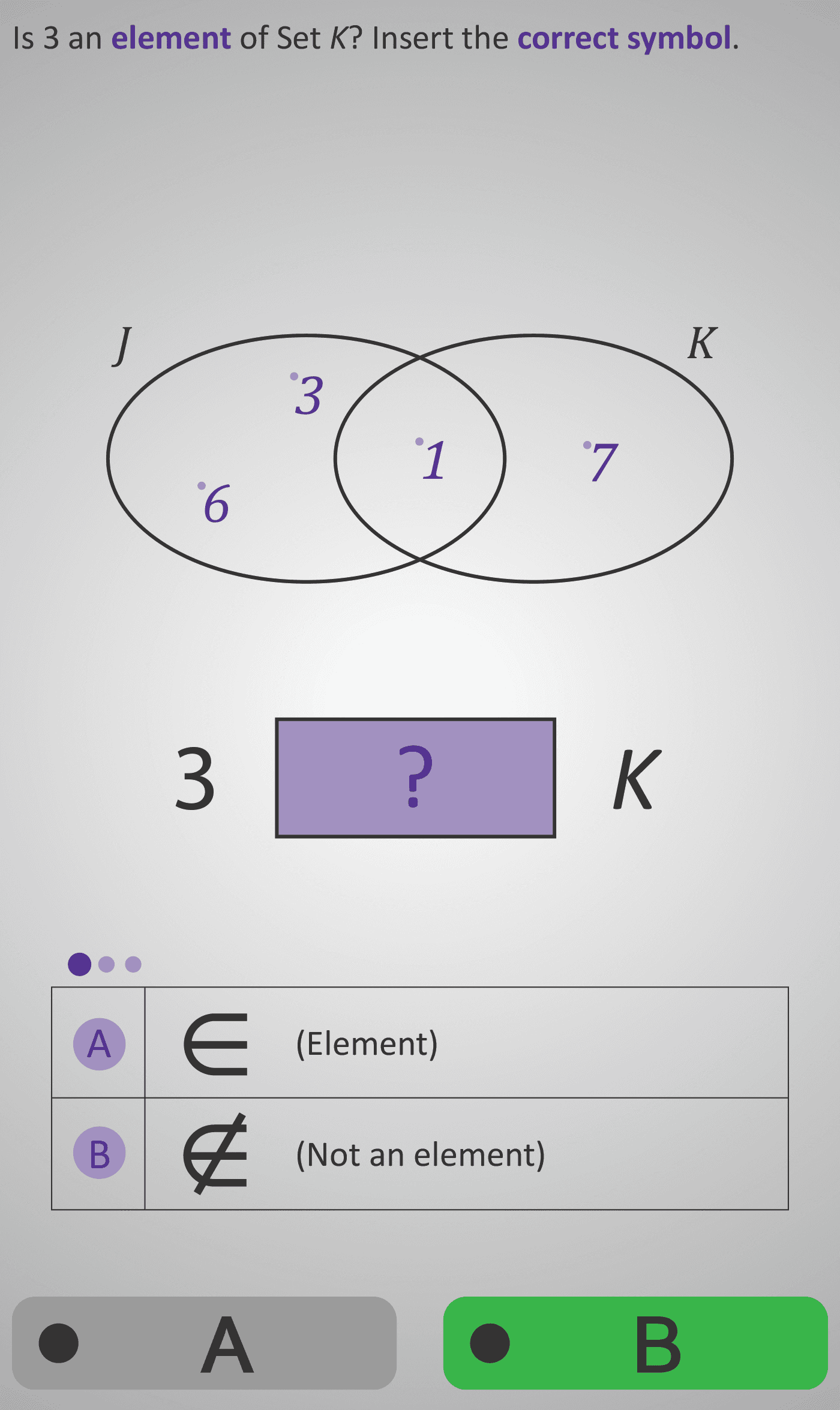
In this Phlow, learners build a deeper understanding of set membership by linking visual and symbolic reasoning. Using a Venn Diagram showing two overlapping sets, J and K, students decide whether particular numbers belong to each set and represent their findings using the symbols ∈ (“is an element of”) and ∉ (“is not an element of”).
Example questions include “Is 3 an element of Set K?” or “Is 1 an element of Set J?”. Each task isolates one logical relationship — identifying whether a specific element lies inside or outside a set — allowing learners to focus entirely on the concept of membership.
This activity bridges visual understanding and formal mathematical notation. By the end, learners can confidently express set relationships using symbols and diagrams, preparing them for later work with intersection (∩), union (∪), and complement (′) notation.
- Interpret whether numbers belong to given sets in Venn Diagrams.
- Use the correct symbols (∈, ∉) for membership notation.
- Connect visual representations with symbolic reasoning.
- Strengthen understanding of set structure and logical inclusion.
Prerequisite Knowledge Required
- Awareness that sets group related items or numbers.
- Ability to interpret elements in a Venn Diagram (from Venn Diagram 3A–3C).
- Familiarity with basic symbolic ideas (e.g. =, ≠).
- Understanding of positional reasoning (inside vs. outside a set).
- Linked earlier Phlows: Venn Diagram 3A – Identifying Elements; Venn Diagram 3B – Overlaps; Venn Diagram 3C – Subsets.
Main Category
Data and Probability → Sets and Symbols
Estimated Completion Time
Approx 7–10 seconds per question (30 total). Total time: 3–5 minutes.
Learning Outcomes
- Identify whether a number is an element of a set using visual reasoning.
- Use ∈ and ∉ correctly to represent membership or exclusion.
- Relate Venn Diagram positions to symbolic notation accurately.
- Develop logical fluency in mathematical set language.
Cognitive Load / Step Size
Low to moderate — each question involves one element and one set, minimising extraneous load. The consistent structure and immediate visual feedback strengthen automatic recall of symbols and reinforce understanding through repetition.
Language & Literacy Demand
Low to moderate — terminology such as element, set, and symbol is presented visually alongside examples. Students engage primarily through visual pattern recognition and symbolic precision rather than text-heavy explanation.
Clarity & Design
- Uncluttered Venn layout with clearly labelled sets J and K.
- Numbers spaced evenly across distinct and overlapping regions.
- Questions displayed clearly (“Is 3 an element of Set K?”).
- Side-by-side comparison of ∈ and ∉ reinforces correct symbol selection.
- Purple highlights guide attention to active set and symbol.
Curriculum Alignment
Strand: Data and Probability → Sets and Relationships
Learning Outcome: Represent and describe elements of sets using diagrams and mathematical notation.
(Aligned with Junior Cycle Mathematics – Strand 1: Number and Relationships, Learning Outcome 1.15.)
Engagement & Motivation
Learners enjoy the quick, puzzle-like format of deciding whether a number belongs to a set. The visual-to-symbolic matching encourages intuitive learning and builds confidence with abstract mathematical language.
Error Opportunities & Misconceptions
- Confusing ∈ (“is in”) with ∉ (“is not in”).
- Assuming elements in the overlap belong to only one set.
- Thinking numbers outside all circles still belong to a set.
Repetition, colour contrast, and feedback-based correction help eliminate these confusions, reinforcing accurate symbol use.
Transferability / Real-World Anchoring
Mastery of membership notation supports logical reasoning, coding structures (e.g. “if item in set:”), data classification, and database queries. It builds analytical thinking skills valuable across mathematics, science, and computing.
Conceptual vs Procedural Balance
Conceptual: Understanding the relationship between sets and elements.
Procedural: Choosing the correct symbol (∈ or ∉) to express that relationship.
The dual visual–symbolic design ensures both are reinforced together.
What Your Score Says About You
- Below 15: Still developing awareness of set membership — review meanings of ∈ and ∉.
- 16–22: Good understanding — occasional mistakes in overlap cases.
- 23–29: Consistent accuracy and confident use of set symbols.
- 30 / 30: Mastery — fluent, logical, and precise in expressing membership relationships.