Volume (L × W × D) 3C
Overview
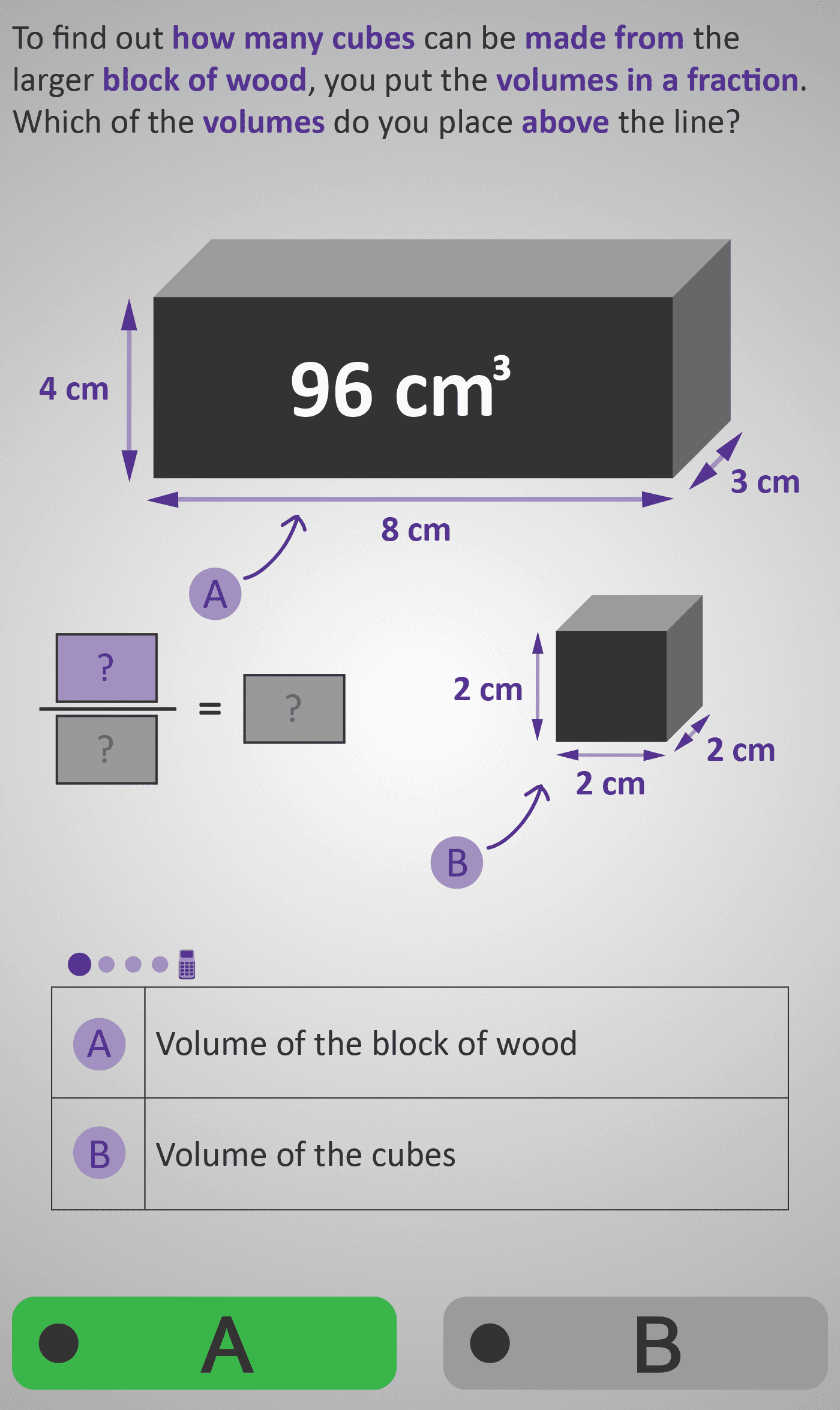
In this Phlow, learners extend their understanding of volume by exploring how division applies to three-dimensional space. They begin by finding the volume of a large rectangular block (e.g. 8 cm × 3 cm × 4 cm = 96 cm³) and the volume of a smaller cube (e.g. 2 cm × 2 cm × 2 cm = 8 cm³).
The Phlow then guides students through comparing these two volumes using a fraction structure — placing the larger block’s volume above the line and the smaller cube’s volume below. Dividing 96 by 8 reveals that 12 smaller cubes can fit inside the larger block.
This approach deepens understanding of division as repeated equal grouping, now applied in three dimensions. Students learn how volume comparison links multiplication (building space) and division (partitioning space), reinforcing flexible reasoning and problem-solving in spatial contexts.
- Calculate how many smaller cubes fit inside a larger block.
- Use division to compare two volumes.
- Construct and interpret volume ratios using fraction form.
- Understand why the total volume is placed above the line when dividing.
Prerequisite Knowledge Required
- Ability to calculate the volume of a cube or cuboid using L × W × H.
- Understanding that division represents sharing or equal grouping.
- Knowledge that cm³ measures 3D space.
- Familiarity with using a calculator for larger multiplication and division.
- Linked earlier Phlows: Volume 3A – Identifying Dimensions (L, W, H); Volume 3B – Calculating and Converting Volume; Divide 2C – Dividing Groups into Equal Parts.
Main Category
Measurement → Volume and Capacity
Estimated Completion Time
Approx 10–15 seconds per question (30 total). Total time: 5–7 minutes.
Learning Outcomes
- Determine how many smaller cubes fit into a larger cuboid using volume division.
- Apply division to relate total and unit volumes.
- Represent volume relationships using fractions.
- Explain the logic behind numerator (larger volume) and denominator (smaller cube).
Cognitive Load / Step Size
Moderate — students progress through three clear stages: calculating each volume, constructing a comparison fraction, and dividing. The visual alignment of block and cube diagrams provides strong scaffolding and ensures minimal working-memory demand.
Language & Literacy Demand
Medium — students encounter terms like block of wood, cube, fraction, and divide. Consistent phrasing (“large block divided by small cube”) and purple visual highlighting help connect symbols (÷, /) with conceptual meaning.
Clarity & Design
- Side-by-side 3D visuals of block and cube clarify proportional relationships.
- Fraction layout shows conceptual comparison before calculation.
- Calculator prompts encourage autonomy and procedural fluency.
- Clean diagrams maintain focus on reasoning rather than decorative detail.
Curriculum Alignment
Strand: Measurement → Length, Area, and Volume
Learning Outcome: Students solve problems involving 3D volume and understand how multiplication and division relate in three-dimensional contexts.
(Aligned with Junior Cycle Mathematics – Strand 2: Geometry and Measurement, Learning Outcomes 2.13, 2.15 & 2.18.)
Engagement & Motivation
The “block of wood” scenario provides tangible, hands-on relevance. Learners experience discovery as they realise how division reverses multiplication in spatial contexts, creating a satisfying “aha” moment.
Error Opportunities & Misconceptions
- Reversing numerator and denominator (putting the cube volume above the block volume).
- Confusing area (cm²) with volume (cm³).
- Interpreting division as calculating a new volume instead of number of cubes.
- Multiplying instead of dividing when comparing two 3D measurements.
The Phlow’s visual ratio layout and guided text explicitly prevent these errors, reinforcing correct logical structure.
Transferability / Real-World Anchoring
This concept connects directly to partitioning materials, designing packaging, or measuring how many equal parts fit into a whole — skills used in manufacturing, architecture, and environmental studies. Understanding how division applies in 3D prepares students for more complex design and engineering tasks.
Conceptual vs Procedural Balance
Conceptual: Understanding division as partitioning space into equal volumes.
Procedural: Applying formulas and performing calculations accurately.
The visual ratio model bridges conceptual and numeric reasoning, reinforcing mastery.
What Your Score Says About You
- Below 15: Beginning to connect multiplication and division in 3D contexts.
- 16–22: Understands total-to-unit relationships but may reverse division order.
- 23–29: Fluent in setting up and solving 3D division problems.
- 30 / 30: Mastery — confidently divides 3D space and interprets ratios of volume with precision.