Algebra 4J

Overview

In this Phlow, learners deepen their understanding of the distributive property by expanding and simplifying expressions that include both variables and constants. Examples like a(a + 5) + 7(a − 2) show how multiplying variables can produce squared terms and new algebraic structures.

Students are guided step-by-step:

Multiply a × a to form a².
Multiply a × 5 to get 5a.
Multiply 7 × a to get 7a.
Multiply 7 × (−2) to form −14.

Learners then combine like terms to simplify the result: a² + 5a + 7a − 14 = a² + 12a − 14. Each multiplication is isolated through guided prompts such as “Multiply 7 by a — what does that equal?” and “Is the sign plus or minus?”.

This structured sequence helps learners understand how squared and linear terms appear naturally through multiplication, revealing the logical flow from expansion to simplification.

Expand brackets containing both variables and constants.
Apply the distributive law step-by-step with attention to signs.
Combine like terms accurately to simplify the result.
Recognise where squared terms emerge from variable multiplication.

Step 1 / 10

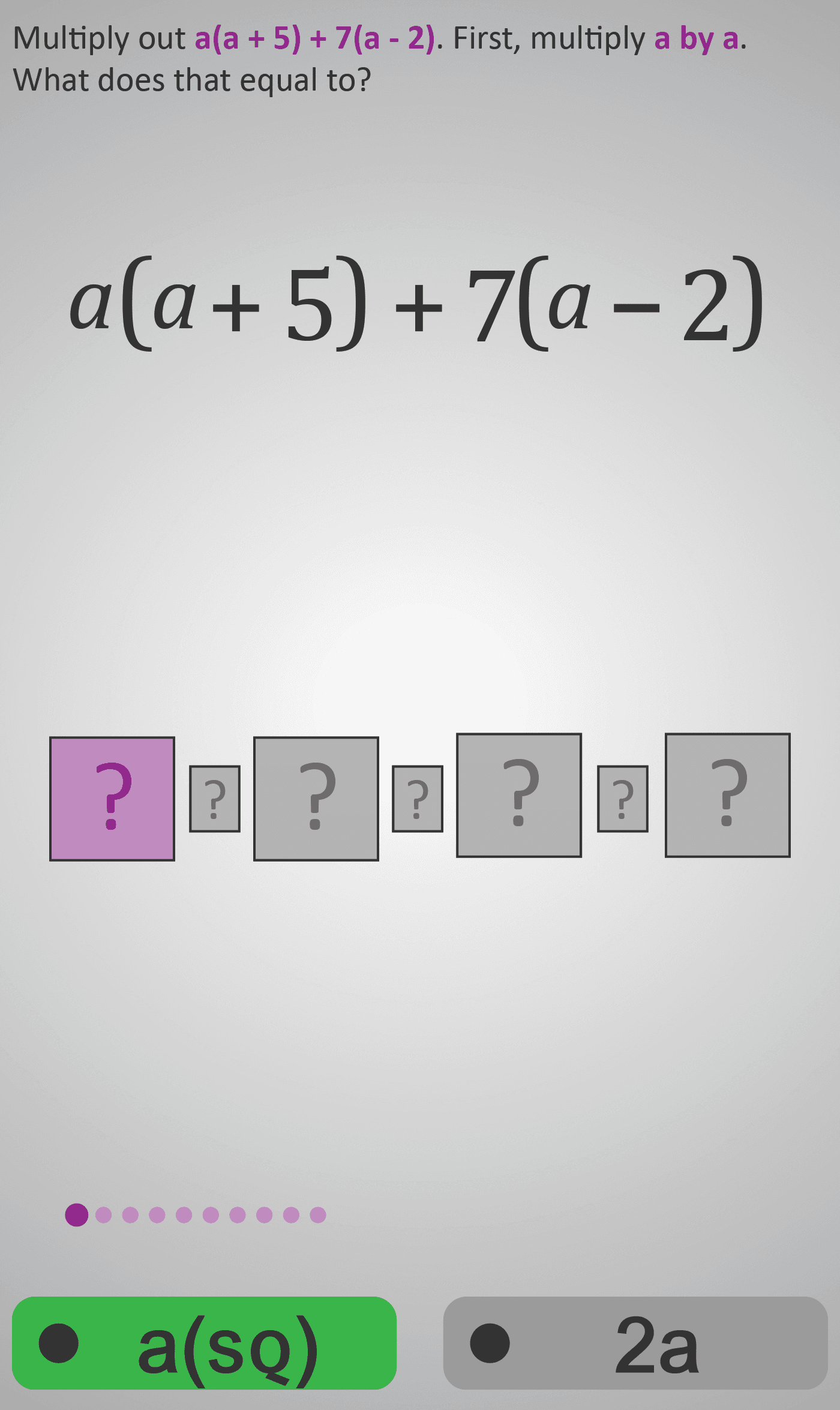
Prerequisite Knowledge Required

Understanding of expanding single brackets (from Algebra 4I).
Familiarity with collecting like terms (from Algebra 4H).
Knowledge of variable multiplication (a × a = a²).
Comfort with positive and negative number operations.
Linked earlier Phlows: Algebra 4H – Simplifying Expressions; Algebra 4I – Expanding and Simplifying Expressions.

Main Category

Algebra → Expanding Brackets → Variables and Simplification

Estimated Completion Time

Approx 9–11 minutes (9 interactive steps).

Learning Outcomes

Expand expressions where variables multiply variables.
Apply the distributive property correctly with positive and negative signs.
Identify and combine like terms after expansion.
Recognise that a² terms emerge from variable–variable multiplication.

Cognitive Load / Step Size

Moderate–High — introducing squared terms raises complexity, so the Phlow slows progression and isolates each multiplication visually. Sign and term prompts reduce errors and maintain flow without overloading learners.

Language & Literacy Demand

Medium — vocabulary such as “expand,” “simplify,” “distributive property,” and “squared” is reinforced visually. Purple-highlighted terms and consistent prompts help learners build language fluency alongside symbol understanding.

Clarity & Design

Each multiplication appears step-by-step, with immediate visual feedback.
Colour-coded signs and coefficients clarify structure.
Interactive “sign choice” questions ensure active engagement.
The full expression builds incrementally, reinforcing procedural and conceptual understanding.

Curriculum Alignment

Strand: Algebra

Learning Outcome: Students expand and simplify algebraic expressions involving more than one bracket, recognising the structure of quadratic terms.

(Aligned with Junior Cycle Mathematics – Strand 3: Algebra, Learning Outcomes 3.6 & 3.7.)

Engagement & Motivation

Learners experience success through guided progress — one bracket at a time. The moment when a × a becomes a² gives a tangible “aha” experience, showing how complexity can emerge from simple patterns.

Error Opportunities & Misconceptions

Forgetting to multiply all terms inside brackets.
Dropping negatives when expanding expressions like 7(a − 2).
Misinterpreting a × a as 2a instead of a².
Combining constants and variables incorrectly (e.g., 5a − 14 → 9a).

Guided cues and intermediate checks catch these common mistakes early, ensuring learners see and correct their thinking in real time.

Transferability / Real-World Anchoring

Understanding how variables multiply supports quadratic reasoning used in physics, architecture, coding, and design. Students see that algebraic rules are universal tools for describing relationships and patterns.

Conceptual vs Procedural Balance

Strongly balanced — learners follow a clear procedure (expand → combine → simplify) while developing conceptual insight into why squared terms form and how algebraic expressions grow in structure.

What Your Score Says About You

Below 20: Needs reinforcement of variable multiplication and sign control.
21–30: Understands the distributive law but sometimes mixes coefficients or signs.
31–39: Expands and simplifies accurately with clear structural reasoning.
40 / 40: Mastery — confidently expands, simplifies, and explains how squared terms arise in algebraic form.