Angles 4B
Overview
In this Phlow, learners explore the fundamental relationship between the three angles of a triangle. They discover that the sum of the interior angles of any triangle equals 180° and use this knowledge to calculate unknown angles through simple subtraction.
Using an example triangle with angles of 85°, 58°, and x°, students are guided step by step:
- Recognising that all interior angles together total 180°.
- Writing this relationship as an equation: x° + 85° + 58° = 180°.
- Rearranging the equation to isolate the unknown angle x°.
- Calculating the missing value: x° = 180° − (85° + 58°) = 37°.
The activity links conceptual understanding with procedural fluency. Learners visualise why the rule holds (angles forming a straight line) and practise how to apply it to different triangles. By combining diagrams, reasoning, and arithmetic, this Phlow builds strong geometric intuition.
- Recall that the sum of angles in a triangle equals 180°.
- Write and rearrange an equation to find an unknown angle.
- Perform subtraction accurately to calculate the missing value.
- Explain the link between the 180° triangle rule and the straight-line property.
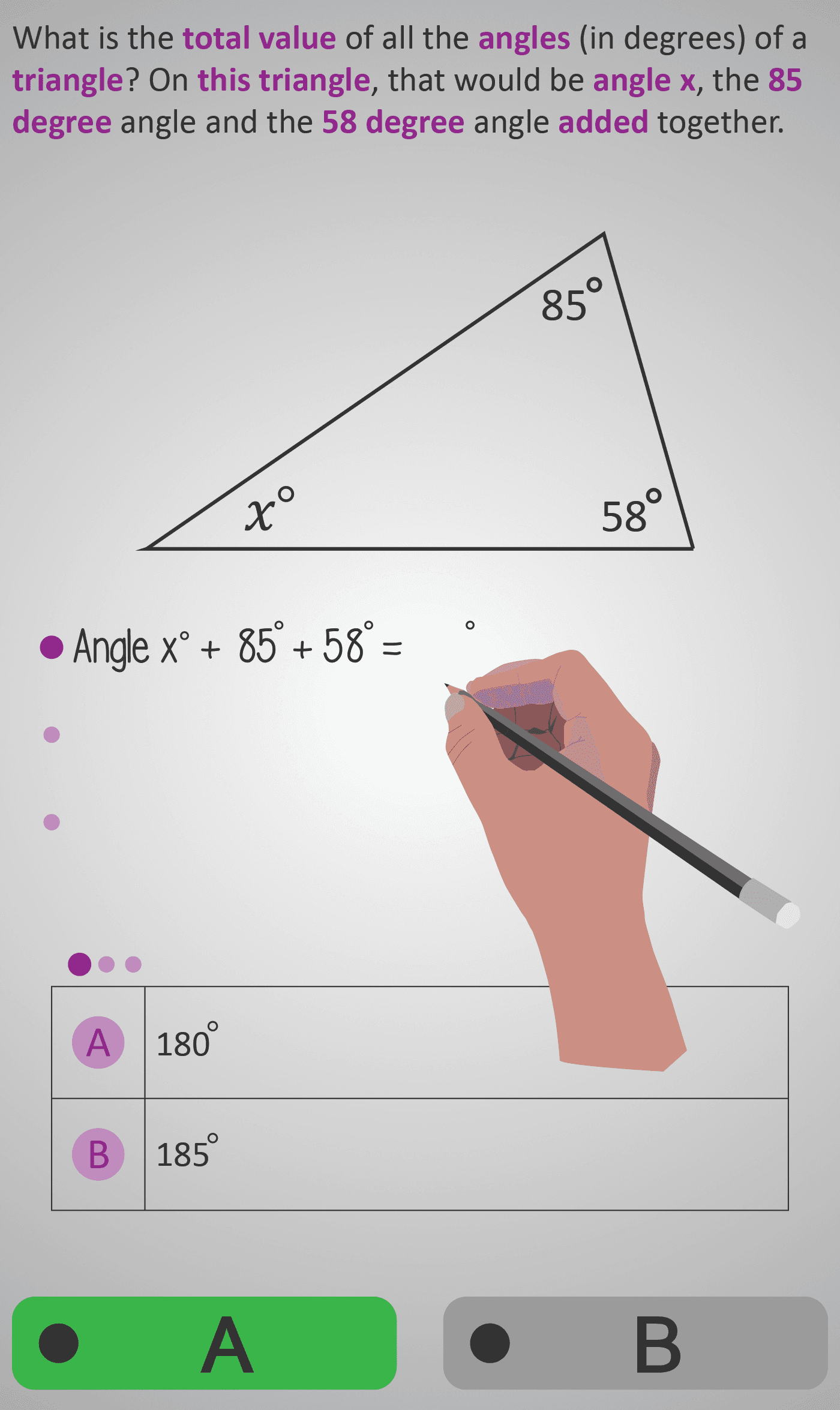
Prerequisite Knowledge Required
- Understanding that angles represent turns and are measured in degrees (°).
- Knowing that a straight line measures 180°.
- Ability to add and subtract whole numbers up to three digits.
- Recognising that a triangle has three sides and three interior angles.
- Linked earlier Phlows: Angles 4A – Opposite and Supplementary Angles; Angles 3C – Classifying Angles (Right, Acute, Obtuse); Shapes 3B – Identifying Triangles by Angle Type.
Main Category
Geometry → Angles → Angles in a Triangle
Estimated Completion Time
Approx 8–10 minutes (3–4 guided interactions).
Learning Outcomes
- State and apply the rule that the interior angles of a triangle sum to 180°.
- Write a simple equation linking the three angles.
- Rearrange the equation to calculate an unknown angle.
- Explain how this relates to the 180° straight-line rule.
Cognitive Load / Step Size
Low–moderate — the Phlow introduces a single new rule and keeps numbers simple. The same diagram and layout are used throughout to minimise working-memory load while reinforcing consistent reasoning patterns.
Language & Literacy Demand
Medium — vocabulary such as “sum,” “total,” “missing angle,” and “added together” is repeated and reinforced visually through highlighted degrees and consistent sentence structure.
Clarity & Design
- Hand-drawn triangle visuals replicate classroom explanation style.
- Each screen isolates one step — write, rearrange, substitute, solve.
- Visual highlighting and colour-coded values strengthen focus on reasoning sequence.
- Encourages both mental and written calculation approaches.
Curriculum Alignment
Strand: Geometry and Trigonometry
Learning Outcome: Students identify and use relationships between angles in a triangle and on a straight line, applying the 180° rule in reasoning and problem solving.
(Aligned with Junior Cycle Mathematics – Strand 3: Geometry and Trigonometry, Learning Outcome 3.3.)
Engagement & Motivation
Students enjoy the sense of discovery as they “uncover” the missing angle. The guided reasoning transforms a memorised rule into something they can see and explain. Immediate feedback and simple calculations sustain focus and confidence.
Error Opportunities & Misconceptions
- Forgetting that the total of triangle angles is 180° (sometimes assuming 360°).
- Adding instead of subtracting when rearranging.
- Subtracting in the wrong order (e.g., 58° − 180°).
- Misidentifying which angle is unknown if the triangle is drawn differently.
Clear question phrasing and sequential highlighting guide students to avoid these mistakes, ensuring both understanding and procedural accuracy.
Transferability / Real-World Anchoring
This principle applies across engineering, architecture, and navigation. Understanding that triangles have fixed angle relationships supports construction, map reading, and problem solving in design and real-world geometry.
Conceptual vs Procedural Balance
Balanced — learners first explore why the rule works (conceptual), then practise how to apply it (procedural) through subtraction and reasoning. Step-by-step visuals ensure comprehension before automation.
What Your Score Says About You
- Below 20: Knows triangles have three angles but not the 180° relationship.
- 21–30: Understands the rule but may struggle with rearranging or subtraction.
- 31–39: Accurately applies subtraction to find missing angles.
- 40 / 40: Mastery — confidently explains and calculates using the 180° triangle rule.