Area 4A

Overview

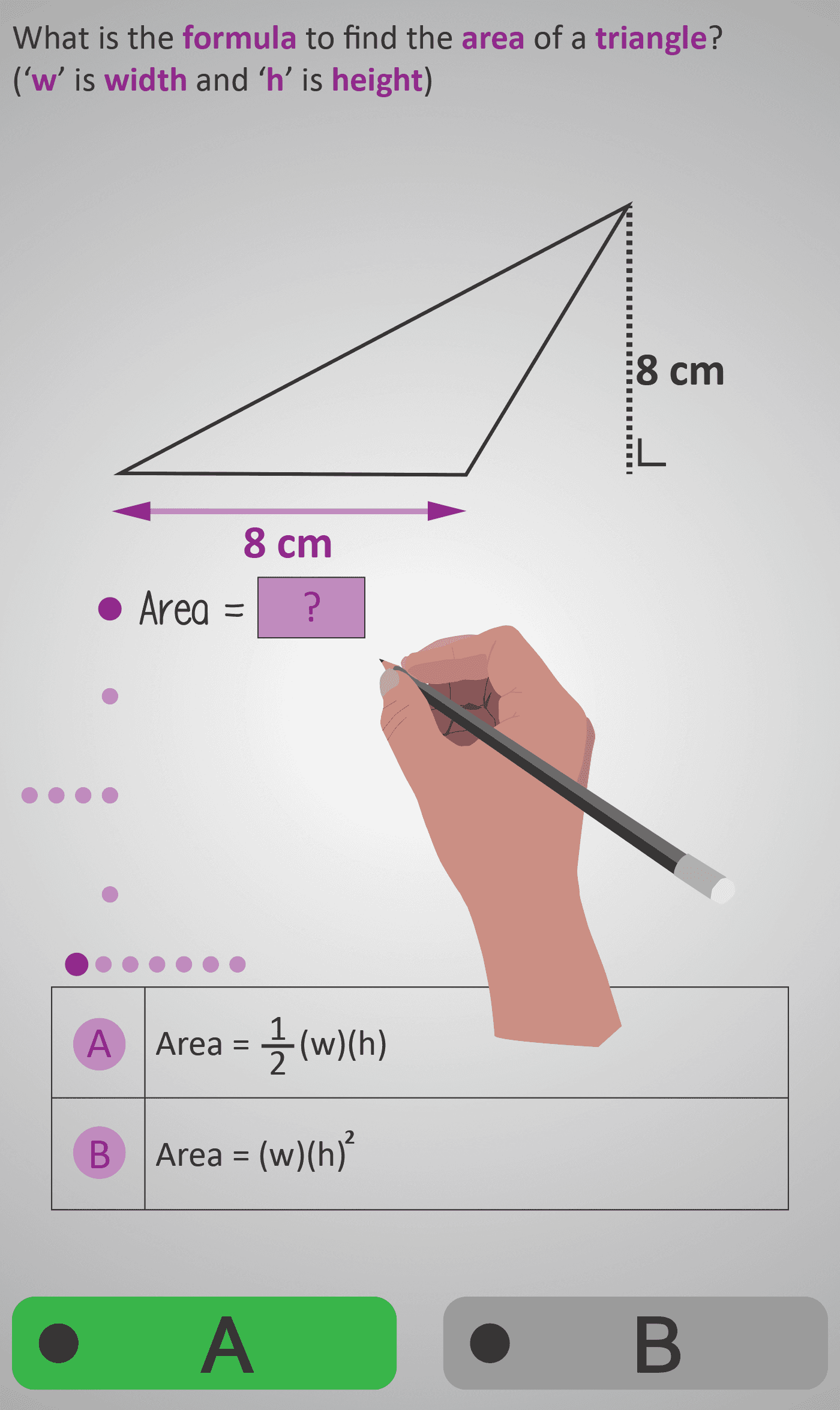
In this Phlow, learners explore how to calculate the area of a triangle step by step using the formula:

Area = ½ × base × height

Students begin by identifying the base (width) and height (perpendicular distance) before substituting values into the formula. Using an example where both base and height are 8 cm, they work through each stage carefully:

Substitute values: Area = ½ × 8 × 8
Multiply: 8 × 8 = 64
Divide by 2: 64 ÷ 2 = 32
Final answer: Area = 32 cm²

Each step is shown visually and algebraically, linking geometry and algebraic reasoning. Hand-drawn working illustrates how the calculation unfolds, reinforcing the meaning of brackets, fractions, and multiplication symbols. Students learn that the triangle’s area formula derives from halving the area of a rectangle with the same base and height.

Recall and write the area formula for a triangle.
Substitute given base and height values correctly.
Simplify expressions involving fractions and brackets.
Calculate the final area with correct units (cm²).

Step 1 / 7

Prerequisite Knowledge Required

Understanding of multiplication and division, including interpreting ½ as “divide by 2”.
Knowledge of what base and height represent in geometric shapes.
Ability to substitute numerical values into a formula.
Familiarity with squared units (cm², m²).
Linked earlier Phlows: Area 3A – Area of a Rectangle; Fractions 3B – One-Half as Division by Two; Multiplication 3C – Expanding Brackets.

Main Category

Measurement → Area → Triangles

Estimated Completion Time

Approx 10–12 minutes (6 guided steps).

Learning Outcomes

Recall and use the formula Area = ½ × base × height.
Substitute values accurately and follow correct order of operations.
Simplify using multiplication and division fluently.
State answers clearly with correct units (cm², m²).

Cognitive Load / Step Size

Moderate — the Phlow integrates algebraic notation and geometry but introduces each action (substitute → expand → simplify → divide) one at a time. Visual scaffolding and consistent notation keep attention focused.

Language & Literacy Demand

Medium — key mathematical terms (“formula,” “substitute,” “expand,” “simplify,” “divide by two”) appear in short, action-based sentences. Consistent repetition reinforces vocabulary comprehension.

Clarity & Design

Consistent use of purple text for mathematical operations (multiply, divide, height, width).
Step-by-step handwriting animations mirror teacher modelling.
Each stage isolates one reasoning step, reducing visual and cognitive load.
Example values remain small and practical for ease of focus.

Curriculum Alignment

Strand: Measurement

Learning Outcome: Students develop and use formulae to calculate the area of regular shapes, including triangles.

(Aligned with Junior Cycle Mathematics – Strand 4: Measures, Learning Outcome 4.3.)

Engagement & Motivation

Students experience success at each mini-step — recognising the formula, substituting numbers, expanding, and simplifying — creating a clear sense of progress. The guided format mirrors how teachers model multi-step calculations.

Error Opportunities & Misconceptions

Forgetting to divide by 2 after multiplying base × height.
Confusing height with the slanted side.
Mixing up base and height during substitution.
Omitting the square unit (cm²) in the final answer.

Animated worked examples and consistent reminders of units and structure reduce these common errors.

Transferability / Real-World Anchoring

Calculating triangular areas applies directly in architecture, construction, engineering, and design. The skill of substituting into formulas also prepares students for algebraic applications in physics and trigonometry.

Conceptual vs Procedural Balance

Balanced — students understand conceptually why the area is half that of a rectangle while practising the procedural skills of substitution, multiplication, and division.

What Your Score Says About You

Below 20: Recognises the triangle but not yet confident applying the formula.
21–30: Can substitute values but needs practice simplifying and dividing.
31–39: Accurately multiplies, divides, and records units.
40 / 40: Mastery — fully understands and explains why the formula divides by two.