Arrow Diagram 4
Overview
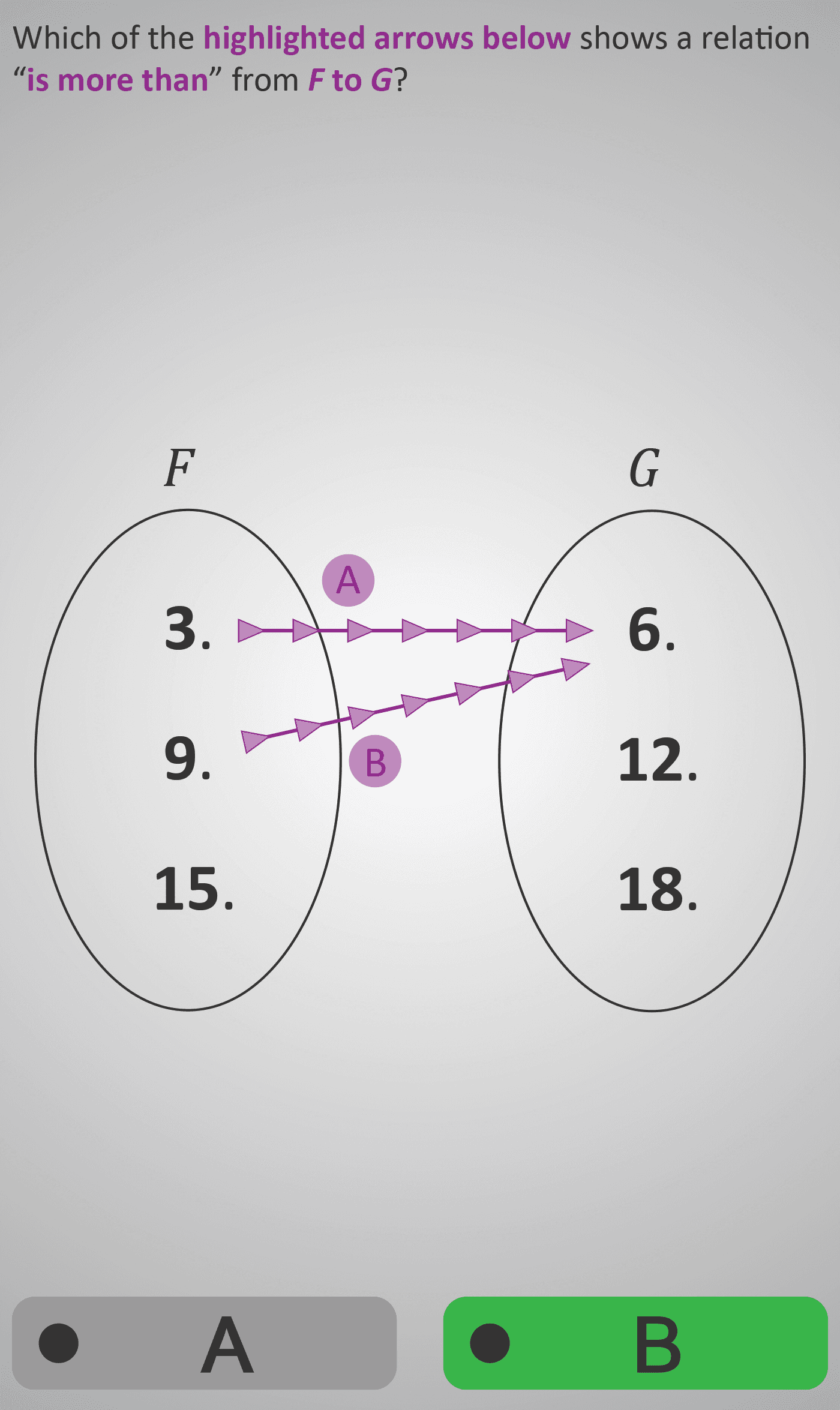
In this Phlow, learners deepen their understanding of relations and mappings using arrow diagrams linking two sets, F and G. Each arrow represents a “couple” (ordered pair) that connects one element from F to one element from G.
Students first practise identifying which element in Set F connects to which in Set G,
tracing arrows and recording the links as ordered pairs — for example, (9, 6) or (15, 12).
They then interpret and reason about relationships such as “is more than,” selecting the arrows that
correctly illustrate this condition.
- Recognise how elements from two sets can be connected by arrows.
- Write ordered pairs to represent these connections.
- Interpret relations such as “is more than” or “is equal to.”
- Develop reasoning about directionality and order within pairs.
The activity bridges visual reasoning and symbolic notation, helping learners connect arrow diagrams to the foundations of coordinate systems and functions.
Prerequisite Knowledge Required
- Recognising and comparing numbers (greater than / less than).
- Understanding what sets and elements are.
- Knowing that ordered pairs are written as (x, y) with direction from first to second element.
- Familiarity with basic arrow diagrams from earlier Phlows.
Linked Phlows
- Arrow Diagram 1A – Introduction to Pairing
- Arrow Diagram 2B – Simple Mapping Between Sets
- Arrow Diagram 3C – Reading and Writing Ordered Pairs
Main Category
Relations and Functions → Representing Relationships → Arrow Diagrams
Estimated Completion Time
Approx. 8–12 seconds per question. 30 questions total (4–6 minutes).
Cognitive Load / Step Size
Medium. Students move from identifying connections to interpreting comparative relationships. Each step reuses the same visual model, maintaining familiarity while increasing reasoning demand.
Language & Literacy Demand
Low. Most tasks rely on visual matching rather than long text. Key terms like “element,” “couple,” and “relation” are introduced contextually and repeated with clear visuals. Comprehension depends on observing arrows rather than reading extended descriptions.
Clarity & Design
- Clean ovals represent Sets F and G with consistent labelling.
- Highlighted arrows (purple for active, grey for inactive) guide attention effectively.
- Each screen focuses on one relation, ensuring clarity and visual precision.
- Simple layout supports understanding without distraction.
Curriculum Alignment
Strand: Algebra
Learning Outcomes:
- 4.2 — Recognise and represent relationships between varying quantities in diagrammatic form.
- 4.3 — Distinguish between types of relations and interpret them using tables, diagrams, and words.
(Aligned with Irish Junior Cycle Mathematics – Strand 4: Algebra)
Engagement & Motivation
The arrow-matching interaction feels like solving a logic puzzle. The instant feedback — with arrows lighting up when correct — gives students a clear sense of progress and accuracy. The simplicity of the visual flow keeps engagement high while introducing abstract concepts.
Error Opportunities & Misconceptions
- Confusing the order of elements (writing (y, x) instead of (x, y)).
- Reading arrows backward (G → F instead of F → G).
- Misinterpreting “is more than” and reversing comparison logic.
- Forgetting to include all pairs when multiple arrows exist.
Guided questioning and visual feedback reinforce the correct direction and structure of ordered pairs.
Transferability / Real-World Anchoring
High. The concept of pairing and directionality prepares students for coordinates, input-output tables, and function mapping. It also strengthens skills in recognising relationships within datasets and graphs.
Conceptual vs Procedural Balance
Balanced, leaning conceptual — students go beyond listing pairs to reasoning about how and why relationships form between sets. The visual model supports abstraction needed for future algebraic and graphical reasoning.
Learning Objectives Addressed
- Identify and record pairs of related numbers from an arrow diagram.
- Understand the direction and structure of ordered pairs (x, y).
- Recognise relations such as “is more than” in visual form.
- Develop foundational mapping concepts for later algebra and coordinate geometry.
What Your Score Says About You
- Below 20: Still learning to trace arrows and record ordered pairs correctly.
- 21–29: Can identify couples but may confuse direction or comparison.
- 31–39: Understands both notation and relational meaning with good accuracy.
- 40 / 40: Mastery — interprets mappings fluently and ready for coordinates and functions.