Co-ordinate 4B

Overview

In this Phlow, learners extend their understanding of coordinate geometry by finding the distance between two points using Pythagoras’s theorem. Through a structured visual walkthrough, they connect algebraic formulas to spatial reasoning on a coordinate grid.

Students begin by identifying horizontal and vertical distances between points (e.g., |ML| = 10 units, |NL| = 5 units) and visualising these as the sides of a right-angled triangle. They then substitute these values into the Pythagorean relationship:

|MN|² = |ML|² + |NL|²

Each step builds logically — first squaring both lengths (10² + 5² = 100 + 25 = 125), then adding them, and finally taking the square root (|MN| = √125 ≈ 11.18).

This process transforms abstract formula memorisation into visual, sequential reasoning. By linking the geometry of the grid with algebraic calculation, learners gain confidence interpreting formulas and using calculators precisely.

Measure horizontal and vertical distances between two coordinates.
Apply Pythagoras’s theorem to find the diagonal distance.
Square, add, and take square roots systematically.
Connect visual, numeric, and symbolic forms of reasoning.

Step 1 / 8

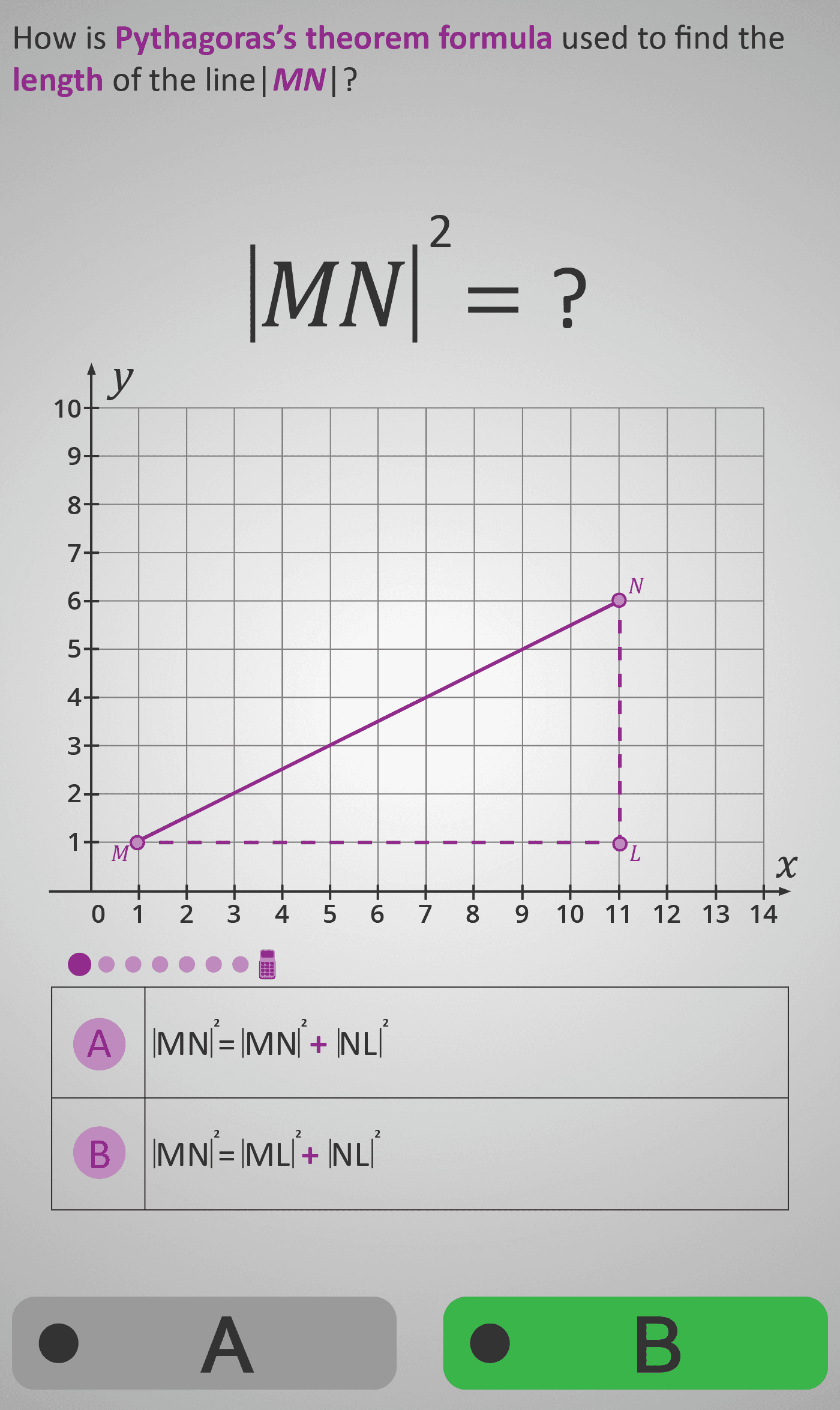
Prerequisite Knowledge Required

Understanding of coordinate grids and plotting points (x, y).
Knowledge of square numbers and square roots.
Recognition of right-angled triangles and their sides (hypotenuse, base, height).
Familiarity with basic calculator operations for squaring and rooting.

Supports Development Of

Conceptual understanding of Pythagoras’s theorem.
Spatial reasoning using coordinates and right angles.
Sequential, multi-step mathematical problem solving.
Confidence translating between geometric and algebraic representations.

Main Category

Geometry → Coordinate Geometry → Distance & Pythagoras’s Theorem

Estimated Completion Time

Approx. 10–14 seconds per screen. 7 screens total. Total time: 4–6 minutes.

Cognitive Load / Step Size

Moderate. Each question isolates a single reasoning step — substituting, squaring, adding, or taking roots — creating a clear mental flow. The stepwise build keeps intrinsic load manageable while promoting deep understanding of the theorem’s logic.

Language & Literacy Demand

Low–Medium. Mathematical symbols (|MN|, ², √) are introduced visually alongside words. Purple-highlighted terms (length, right angle, Pythagoras’s theorem) support vocabulary acquisition while maintaining focus on mathematical reasoning rather than reading load.

Clarity & Design

Clear symmetry between geometric diagrams and algebraic notation.
Colour-coded triangle sides connect directly to equation parts.
Handwritten working reinforces procedural order and authenticity.
Calculator and square-root icons prompt accurate operation sequencing.

Curriculum Alignment

Strand: Geometry and Trigonometry (Junior Cycle Mathematics)

3.7 — Determine distance between points using coordinates.
3.8 — Apply Pythagoras’s theorem to right-angled triangles.
3.9 — Use coordinate geometry to solve geometric problems.

Engagement & Motivation

High. The progression from simple measurements to calculated discovery creates a satisfying “aha” moment. Visualising abstract algebraic steps through familiar grid diagrams sustains motivation and confidence throughout.

Error Opportunities & Misconceptions

Forgetting to square both side lengths before adding.
Confusing the hypotenuse with one of the shorter sides.
Using x and y coordinate differences incorrectly (reversed or mismatched).
Taking the square instead of the square root at the final step.

Transferability / Real-World Anchoring

Strong. This skill applies directly to navigation, mapping, measurement, and computer graphics. It also forms a foundation for trigonometry, vectors, and future problem solving in engineering, physics, and design.

Conceptual vs Procedural Balance

Balanced. Learners practise the procedure of applying Pythagoras’s theorem while developing a conceptual understanding of how distances emerge from geometric relationships on a coordinate plane.

Learning Objectives Addressed

Apply Pythagoras’s theorem to find distances between two points.
Translate between visual grids and algebraic formulas.
Use calculator operations confidently for square and root calculations.
Develop spatial reasoning through geometric problem-solving.

What Your Score Says About You

Below 20: You’re beginning to connect coordinates and distance — review squaring and adding steps.
21–29: You follow the process correctly but need more precision in squaring and rooting.
30–39: You’re fluent with Pythagoras’s theorem and calculator use.
40 / 40: You’ve mastered coordinate distance calculations — ready for gradients and 3D geometry.