Fraction 4C

Overview

In this Phlow, learners practise calculating a fraction of a quantity using a clear two-step method:

Divide the whole number by the denominator (the number below the line) to find one equal part.
Multiply that result by the numerator (the number above the line) to find the fractional amount.

For example: 3/7 of 35 = (35 ÷ 7) × 3 = 5 × 3 = 15.
This structure reinforces that the denominator represents how many equal parts the whole is divided into, while the numerator tells how many of those parts are taken.

By practising with a range of examples (e.g. 5/6 of 30, 7/11 of 22), learners develop both procedural fluency and conceptual understanding of how fractions operate on whole numbers.

Worked Example

Find 3/7 of 35.
Divide 35 by 7 → 35 ÷ 7 = 5.
Multiply by numerator → 5 × 3 = 15.
Answer: 3/7 of 35 = 15.

Sample Questions

What is 2/5 of 20?
What is 4/9 of 45?
Find 3/8 of 40.
Explain why you divide before multiplying.

This Phlow builds a robust understanding of fractions as operators, linking symbolic, procedural, and conceptual reasoning in one consistent visual framework.

Step 1 / 6

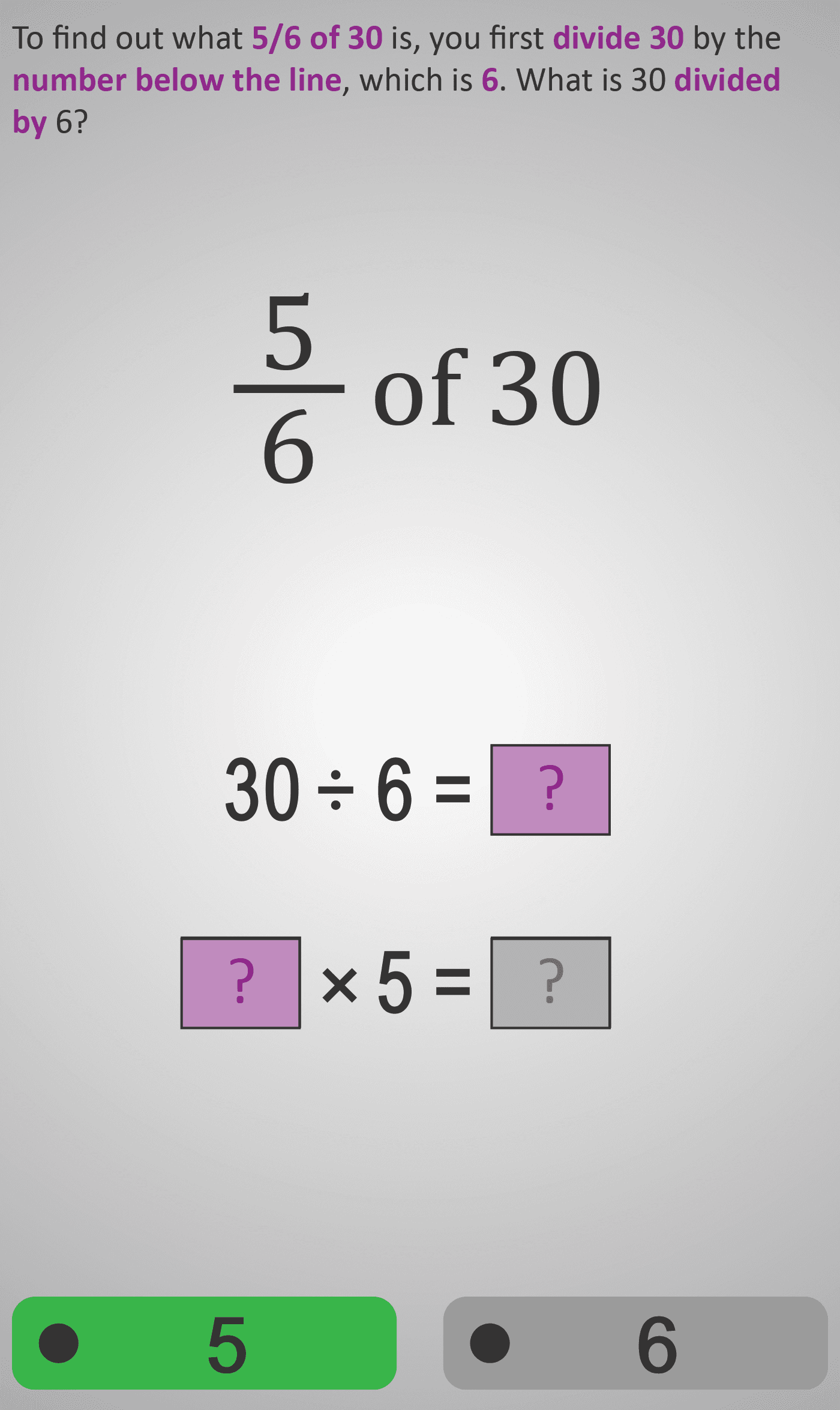
Prerequisite Knowledge Required

Main Category

Number → Fractions and Ratios

Estimated Completion Time

Approx. 10–14 seconds per question.
40 questions total → Total time: 7–10 minutes.

Cognitive Load / Step Size

Moderate to low. The consistent two-step process (divide → multiply) ensures clarity and repetition builds fluency. Colour-coded visuals guide attention and keep the cognitive demand balanced.

Language & Literacy Demand

Low to moderate. Instructions are concise (“divide by…”, “multiply by…”). Vocabulary is limited to key fraction terms (“above the line”, “below the line”), making it accessible for all literacy levels.

Clarity & Design

Purple emphasis distinguishes action words from numerical content.
Each screen isolates one reasoning step to prevent overload.
Large, centred layout enhances focus on sequence and accuracy.
Minimal design maintains focus on the logic of the two-step method.

Curriculum Alignment (ROI Junior Cycle Mathematics)

Strand: Number
Strand Unit: Fractions – Equivalence and Operations
Learning Outcomes:

Understand fractions as operators (e.g., “¾ of a set”).
Apply multiplication and division to find a fraction of a quantity.
Relate the process to proportional reasoning and scaling.
Demonstrate understanding of part–whole relationships numerically.

Engagement & Motivation

High. Each task is fast and rewarding, providing immediate visual confirmation. Real-world “of” phrasing (e.g. ⅔ of a group) enhances practical relevance and confidence.

Error Opportunities & Misconceptions

Multiplying before dividing.
Reversing numerator and denominator.
Assuming “of” always means multiply directly.
Skipping division or rounding too early.

Transferability / Real-World Anchoring

Strong. The concept applies to percentages, ratios, scaling, and data analysis. Students learn that fractions act as operators for real quantities (e.g. “⅖ of 100 students”).

Conceptual vs Procedural Balance

Procedural with conceptual reinforcement. While the process is structured, each step is conceptually justified (“divide by denominator”, “multiply by numerator”) ensuring understanding as well as skill.

Learning Objectives Addressed

Compute a fraction of a number accurately using divide → multiply.
Understand the meaning of numerator and denominator in scaling.
Apply reasoning to proportion-based contexts.
Develop fluency and confidence in structured fractional operations.

What Your Score Says About You

Below 20: You may be multiplying before dividing — revisit the step order carefully.
21–29: You understand the process but need more consistency and fluency.
31–39: Strong understanding and accuracy with fractions of numbers.
40 / 40: Excellent! You’ve mastered finding fractions of quantities with confidence.