Net of a Cube 4
Overview
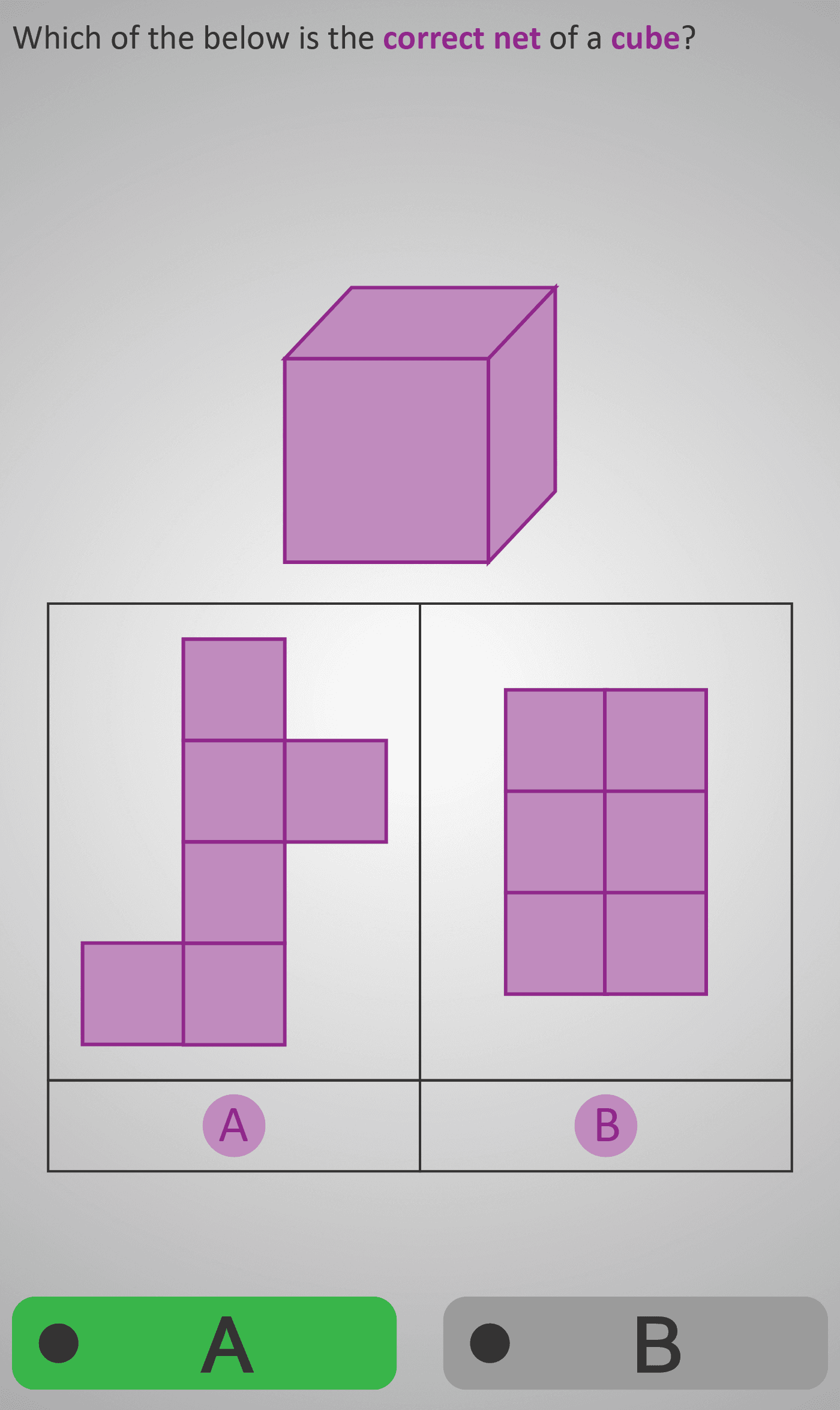
In this Phlow, learners explore how a cube can be unfolded into a 2D net and then re-folded into its 3D form. Each question presents a cube at the top of the screen and two possible nets below (options A and B). Students must decide which net would correctly fold up to form the cube.
Through repeated visual comparisons, learners develop spatial reasoning — the ability to mentally visualise and manipulate shapes in space. They discover that a valid cube net always has six connected squares that meet correctly along edges without overlapping. Early questions show familiar “T-shaped” nets, while later ones introduce rotated or less common configurations that test deeper visual understanding.
By examining how faces connect and predicting foldability, students strengthen geometric intuition and visual–spatial thinking — key skills for geometry, design, and engineering.
Worked Example
A cube has 6 square faces.
Step 1: Each net must contain exactly 6 squares.
Step 2: Check that all squares are connected edge-to-edge (no diagonals).
Step 3: Imagine folding — do all faces meet without overlap?
Example: The “T” shaped net folds into a cube — correct.
A straight-line arrangement does not — incorrect.
Sample Prompts
- Which of the two nets would fold into a cube?
- How many squares does the net need?
- Would these squares overlap when folded?
- What happens if one square is missing or misplaced?
Why This Matters
Visualising 3D shapes from 2D drawings is essential for geometry, design, and real-world problem solving. This Phlow bridges the gap between abstract shape concepts and hands-on spatial reasoning, preparing students for tasks in construction, modelling, and technical drawing.
Prerequisite Knowledge Required
- Understanding of faces, edges, and vertices of 3D shapes.
- Recognition of squares and symmetry.
- Basic awareness of folding and how 2D surfaces form 3D objects.
Linked Phlows:
Shapes 3A–3E – Identifying 2D and 3D Shapes,
Cube 4A – Properties of Cubes and Cuboids,
Nets 3 – Introductory Folding Shapes.
Main Category
Geometry → 3D Shapes and Spatial Reasoning
Estimated Completion Time
Approx. 10–14 seconds per question.
40 questions total → Total time: 7–10 minutes.
| Learner Profile | Estimated Time | Description |
|---|---|---|
| One Level Below | 9–10 min | May visualise folding physically or rotate nets slowly in mind. |
| At Level | 7–8 min | Recognises valid cube nets from face structure and adjacency patterns. |
| One Level Above | 5–6 min | Instantly perceives correct folding and symmetry mentally. |
Cognitive Load / Step Size
Moderate. Each question varies the square arrangement slightly, asking learners to mentally fold and rotate the net. The gradual increase from simple to complex nets maintains cognitive engagement while avoiding visual overload.
Language & Literacy Demand
Low. Questions follow a single, consistent structure (“Which of the below is the correct net of a cube?”). Visual information conveys the concept, making it accessible for students with weaker reading skills or English as an additional language.
Clarity & Design
- Minimalist design — cube at the top, options below — creates visual predictability.
- Purple highlights unify the cube and corresponding net faces.
- High contrast and spacing ensure clarity and focus.
- Design mimics how a teacher would demonstrate cube folding in class.
Curriculum Alignment (ROI Junior Cycle Mathematics)
- Strand: Shape and Space
- Strand Unit: 3D Shapes and Spatial Visualisation
- Learning Outcomes:
- Recognise and describe nets of 3D shapes, particularly cubes.
- Visualise and represent movement between 2D and 3D forms.
- Predict folding and connectivity between faces.
- Develop spatial reasoning and symmetry awareness.
Engagement & Motivation
The challenge of predicting folding outcomes is both visual and interactive. Students experience natural curiosity and satisfaction when visualising a correct net. This form of problem solving engages visual learners and rewards persistence.
Error Opportunities & Misconceptions
- Counting the wrong number of faces (not 6).
- Assuming any 6-square pattern forms a cube.
- Overlooking proper edge connections between faces.
- Failing to distinguish rotated or mirrored nets.
Transferability / Real-World Anchoring
Strong. Understanding nets connects mathematics with real-world design — packaging, model-making, engineering, and architecture. Students learn how flat materials (e.g., cardboard or metal sheets) fold into 3D structures, linking spatial logic with creative design.
Conceptual vs Procedural Balance
Conceptual. Success depends on visual reasoning, not formula memorisation. Learners strengthen conceptual understanding of how 2D representations map onto 3D objects.
Learning Objectives Addressed
- Identify valid cube nets and explain why others do not work.
- Visualise folding and connectivity between faces.
- Develop mental rotation and spatial awareness skills.
- Understand geometric structure through visual problem solving.
What Your Score Says About You
- Less than 20: You may struggle with 3D visualisation — practise folding paper nets to strengthen understanding.
- 21–29: You can identify some cube nets but may need more experience with rotations.
- 31–39: You confidently recognise correct nets and can mentally rotate shapes accurately.
- 40 / 40: Excellent spatial reasoning — strong foundation for geometry, engineering, and design thinking.