Pythagoras’ Theorem 4A
Overview
In this Phlow, learners explore Pythagoras’ theorem through a visual real-world example — a flagpole supported by a rope. They learn that in a right-angled triangle, the square of the hypotenuse equals the sum of the squares of the other two sides.
Each question isolates one reasoning step: identifying the hypotenuse, substituting the side lengths, squaring and adding, taking the square root, and rounding the result. This gradual pacing ensures both understanding and fluency.
Worked Example
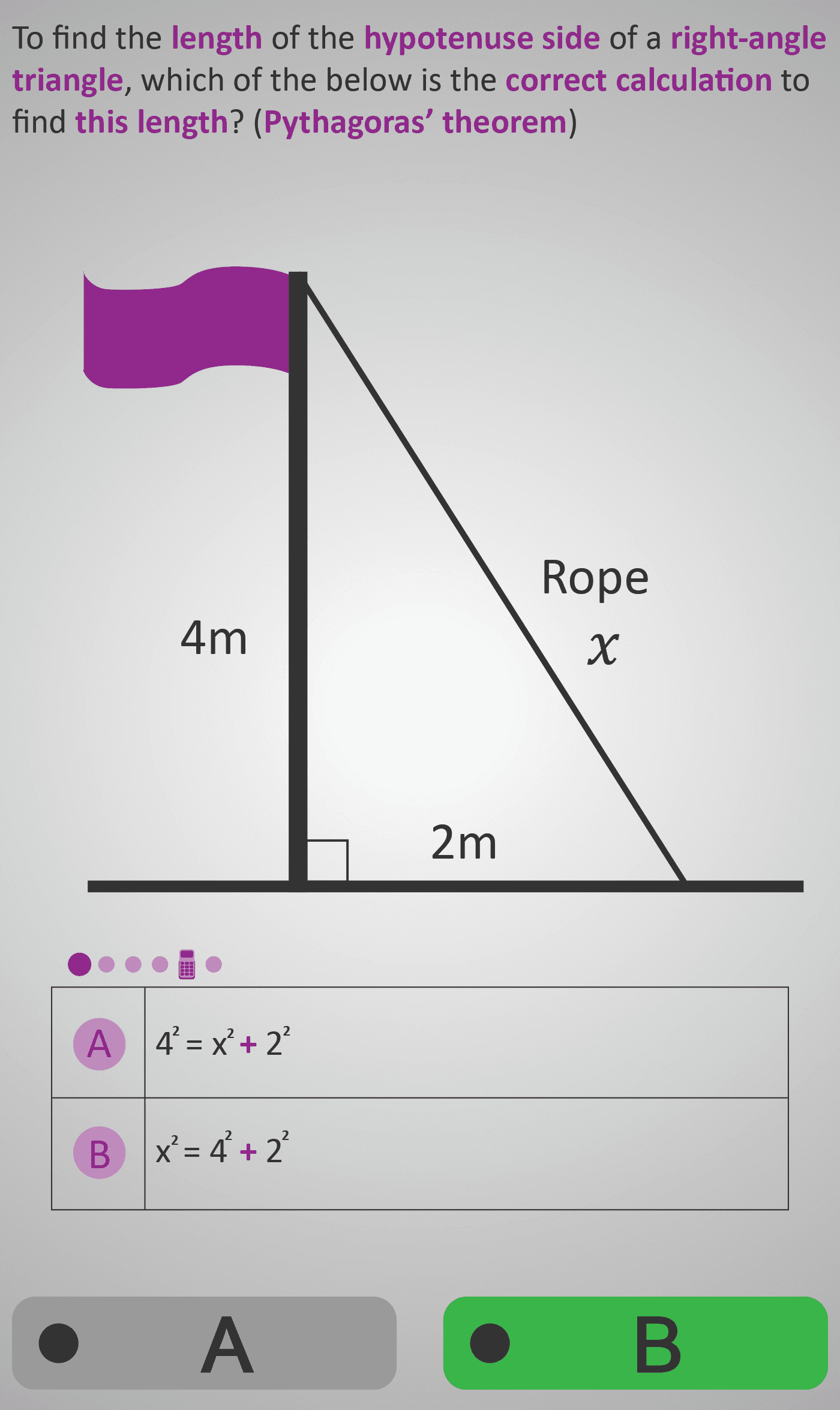
Given: sides 4 m and 2 m
x² = 4² + 2²
x² = 16 + 4
x² = 20
x = √20
x ≈ 4.472…
x ≈ 4.5 m
Step sequence:
- Identify the right angle and label the hypotenuse.
- Write the correct formula:
x² = a² + b². - Substitute side lengths and calculate the sum of squares.
- Take the square root to find
x. - Round to one decimal place and state the length.
Sample Prompts
- Which side is the hypotenuse?
- Which of these equations is correct?
- What is 4² + 2²?
- What is √20 rounded to one decimal place?
Why This Matters
Pythagoras’ theorem is a cornerstone of geometry and physics. Understanding it connects algebraic reasoning with spatial thinking, allowing students to solve practical measurement problems and laying the foundation for trigonometry.
Prerequisite Knowledge Required
- Know how to square and find square roots of numbers.
- Recognise right-angled triangles and identify the hypotenuse.
- Use a calculator to find roots and round results.
Linked Phlows:
Squares & Roots 3A / 3B – Calculating Squares and Roots,
Triangles 3C – Recognising Right-Angled Triangles.
Main Category
Geometry – Right-Angled Triangles
Estimated Completion Time
Approx. 10–14 seconds per question.
40 questions total → Total time: 7–10 minutes.
Cognitive Load / Step Size
Small, deliberate increments. Each new screen introduces one new operation (squaring, adding, rooting, rounding), maintaining focus and reducing working-memory strain.
Language & Literacy Demand
Low to moderate. Terms such as hypotenuse, squared, and square root are reinforced through visuals. Purple highlights (e.g., “x squared”, “length”, “plus”) guide attention and support comprehension.
Clarity & Design
- Uncluttered, hand-drawn visuals showing each working step.
- Flagpole and rope context gives immediate geometric meaning.
- Colour-coded cues and order dots guide the sequence of reasoning.
- Calculator icons reinforce real-world application.
Curriculum Alignment (ROI Junior Cycle Mathematics)
- Strand: Geometry & Trigonometry
- Learning Outcomes: Apply Pythagoras’ theorem to right-angled triangles; understand the relationship between the sides; use square roots to find unknown lengths; round results accurately.
Engagement & Motivation
The realistic rope-and-flagpole example makes maths feel purposeful. Each step reveals progress, encouraging curiosity and confidence as learners watch the calculation unfold visually.
Error Opportunities & Misconceptions
- Placing the hypotenuse on the wrong side of the formula.
- Adding sides before squaring them.
- Forgetting to take the square root.
- Incorrect rounding of the final answer.
Transferability / Real-World Anchoring
Excellent. Students can apply this to ramps, ladders, sports lines, and other real measurements. The reasoning connects geometric structure with algebraic and calculator skills.
Conceptual vs Procedural Balance
Balanced. Learners build conceptual understanding of the theorem’s logic and procedural fluency in calculation, gaining both insight and skill.
Learning Objectives Addressed
- Identify the hypotenuse and apply Pythagoras’ theorem correctly.
- Substitute side lengths and compute unknown sides.
- Use a calculator to find square roots.
- Round to one decimal place and express as a real length.
What Your Score Says About You
- Less than 20: Beginning to connect sides and squares — practise identifying the hypotenuse.
- 21–29: Correct setup but occasional slips with squaring or rounding.
- 31–39: Accurate calculation and clear understanding of the theorem.
- 40 / 40: Mastery — fluent in reasoning, calculation, and accurate rounding.