Pythagoras’ Theorem 4B

Overview

This Phlow builds real-world understanding of Pythagoras’ theorem by comparing two walking routes across a rectangular field — around the edges versus diagonally through it. Learners calculate the diagonal distance using the theorem, round their answer, and find the difference between both paths.

The sequence moves smoothly from computation to reasoning: identifying the formula, substituting values, squaring and adding, taking the square root, rounding, and finally comparing route lengths. Each question isolates one micro-step to keep focus clear.

Worked Example

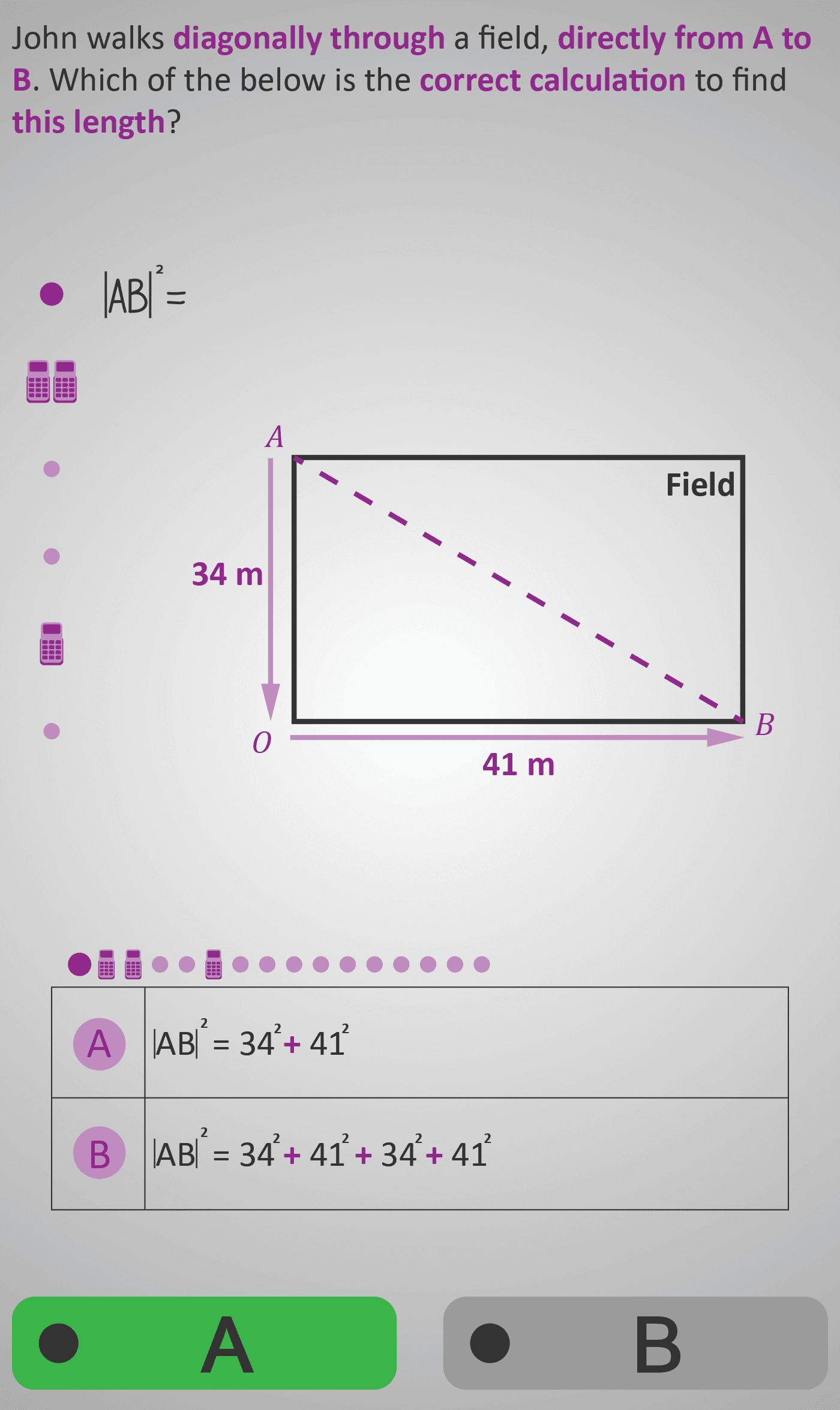
Given: sides = 34 m and 41 m

|AB|² = 34² + 41²
|AB|² = 1156 + 1681 = 2837
|AB| = √2837 ≈ 53.3 m

Around = 34 + 41 = 75 m
Difference = 75 - 53.3 = 21.7 → 22 m shorter

Step sequence:

Identify the two known sides and recall the theorem.
Substitute, square, and add the sides.
Take the square root to find the diagonal length.
Round to one decimal place and compare with the perimeter route.

Sample Prompts

Which side represents the diagonal?
What is 34² + 41²?
What is √2837 rounded to one decimal place?
How much shorter is the diagonal path?

Why This Matters

This Phlow connects abstract geometry to practical decision-making. Learners see how Pythagoras’ theorem answers real questions — like which path is shorter — making mathematical reasoning tangible and relevant.

Step 1 / 16

Prerequisite Knowledge Required

Know how to square and find square roots using a calculator.
Recognise sides of right-angled triangles and identify the hypotenuse.
Be able to perform subtraction and rounding to one decimal or whole number.

Linked Phlows:
Squares & Roots 3A / 3B – Calculating Powers and Roots, Pythagoras’ Theorem 4A – Finding the Hypotenuse, Rounding 3C – Rounding Decimals Accurately.

Main Category

Geometry – Right-Angled Triangles

Estimated Completion Time

Approx. 10–14 seconds per question.
40 questions total → Total time: 7–10 minutes.

Cognitive Load / Step Size

Moderate and well-paced. Each stage adds one reasoning layer — from calculation to interpretation — maintaining clarity and engagement while avoiding overload.

Language & Literacy Demand

Low to moderate. Visuals support every key idea (diagram, colour-coded sides, labels). Terms like diagonal and difference are introduced contextually, ensuring accessibility across literacy levels.

Clarity & Design

Purple dashed diagonal connects the formula to the visual.
Calculator icons guide students through each computation.
Handwritten animations and colour-coded sides reinforce understanding.
Balanced layout keeps attention on geometric reasoning.

Curriculum Alignment (ROI Junior Cycle Mathematics)

Strand: Geometry & Trigonometry
Learning Outcomes: Apply Pythagoras’ theorem to find unknown sides; round results accurately; compare distances in real-world problems; distinguish between exact and approximate answers.

Engagement & Motivation

The “shortcut through the field” problem feels familiar and practical. Each question builds towards a satisfying realisation — that the diagonal is shorter — keeping curiosity and motivation high.

Error Opportunities & Misconceptions

Squaring after addition instead of before.
Forgetting to take the square root.
Confusing the around route with the diagonal route.
Rounding incorrectly or inconsistently.

Transferability / Real-World Anchoring

Very strong. Learners can transfer this reasoning to navigation, sports design, construction, and mapping — any situation comparing direct and indirect paths.

Conceptual vs Procedural Balance

Balanced. Students first apply procedural fluency in the theorem, then reason conceptually about efficiency and interpretation, turning maths into real-world reasoning.

Learning Objectives Addressed

Apply Pythagoras’ theorem to find diagonal distances.
Round results correctly to one decimal and whole number.
Compare real-world distances and calculate differences.
Explain why the diagonal path is shorter than walking around.

What Your Score Says About You

Less than 20: You recall the theorem but may mix up steps or rounding.
21–29: You follow the process but sometimes slip in accuracy or interpretation.
31–39: You calculate confidently, compare effectively, and round accurately.
40 / 40: Excellent — you master both the procedure and the reasoning behind it.