Patterns 4E

Overview

In this Phlow, learners explore a linear relationship within a meaningful real-world context: Dominik’s medicine bottle empties by the same amount each day.

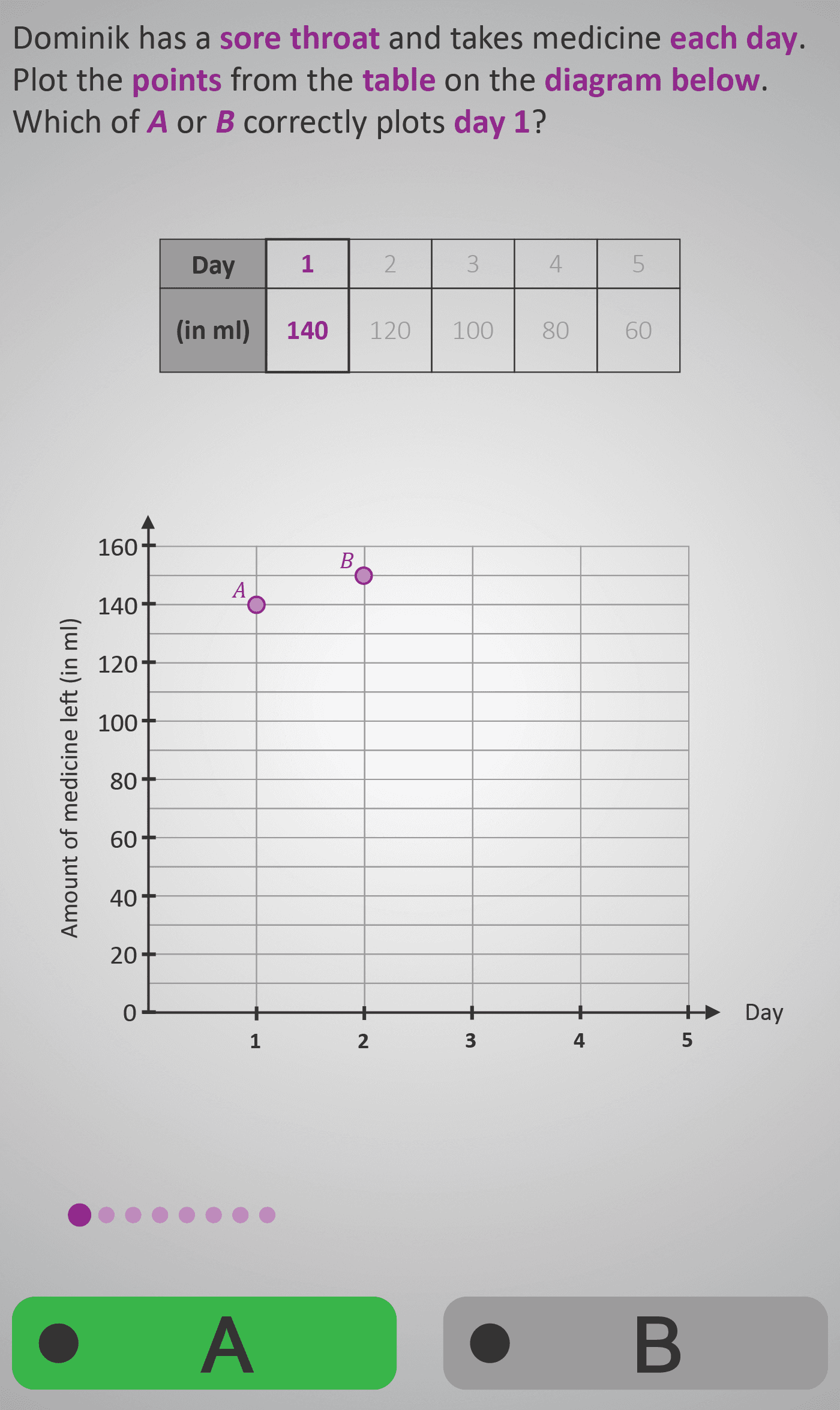
Students begin with a table of data showing the number of days and the amount of medicine left in millilitres (ml). They then plot these values as points on a coordinate grid to visualise the relationship between time (x-axis) and remaining quantity (y-axis).

Each plotted point shows the pattern decreasing by a constant 20 ml per day. This regular change leads to the algebraic rule:

      Amount = 160 − 20d

where d represents the number of days. Students compare this correct equation to incorrect forms such as d + 20 to deepen understanding of how subtraction represents a decrease.

By connecting table → graph → formula, learners build a complete picture of how linear patterns behave and why all the plotted points align on a straight line.

Worked Example

      Table of Data
      --------------
      Day (d) | Amount Left (ml)
         0    |     160
         1    |     140
         2    |     120
         3    |     100
         4    |      80
         5    |      60
         6    |      40
         7    |      20
         8    |       0

      Pattern Rule → Amount = 160 − 20d
      Difference per day → −20 ml

Sample Prompts

How much medicine is left after 3 days?
What is the rate of change in ml per day?
Write an expression for the amount left after d days.
Why do the points form a straight line?

Why This Matters

This Phlow bridges arithmetic sequences and algebraic reasoning. Students learn to recognise and describe constant change across representations — from tables and graphs to symbolic expressions — forming a key foundation for functional thinking and later work on slope–intercept equations.

Step 1 / 8

Prerequisite Knowledge Required

Read coordinate axes and plot ordered pairs (x, y).
Identify increasing or decreasing trends in data tables.
Understand subtraction and multiplication patterns.
Recognise that “linear” means equal change per equal interval.

Linked Phlows:
Patterns & Sequences 4D – Connecting tables and patterns, Graphs 3B – Plotting points on coordinate grids, Algebra 4A – Simple equations and expressions.

Main Category

Algebra / Data & Graphing → Connecting Tables, Graphs, and Equations

Estimated Completion Time

Approx. 10–14 seconds per question.
40 questions total → Total time: 7–10 minutes.

Learner Profile	Estimated Time	Description
One Level Below	9–10 min	Plots by sight but struggles to link points back to table data.
At Level	7–8 min	Plots and interprets linear decrease accurately, recognising the correct rule.
One Level Above	5–6 min	Identifies slope and intercept mentally; generalises beyond given data.

Cognitive Load / Step Size

Moderate. Each stage introduces one representational shift — from table to graph to algebra — but keeps the numerical pattern consistent (−20 ml/day). This clear progression maintains low intrinsic load while building abstraction gradually.

Language & Literacy Demand

Medium. Everyday terms (days, medicine, remaining) pair naturally with mathematical ones (plot, expression, linear). Sentences are short, and purple highlights focus attention on key numbers and words, supporting accessibility for EAL learners.

Clarity & Design

Consistent graph scaling (0–160 ml) aids visual comparison.
Purple accents highlight rate of change and formula structure.
Two formulas (160 − 20d vs d + 20) shown side by side for conceptual contrast.
Sequential plotting animation builds learner confidence and pattern recognition.

Curriculum Alignment (ROI Junior Cycle Mathematics)

Strand: Algebra / Data
Strand Unit: Representing Relationships; Graphing Linear Patterns
Learning Outcomes:

Represent and interpret linear relationships in tables and graphs.
Recognise and describe constant rates of change.
Express relationships using algebraic formulas.
Justify and interpret linear graphs in real-life contexts.

Engagement & Motivation

The relatable scenario (medicine usage) makes linear reasoning meaningful. Students experience real satisfaction as plotted points align perfectly into a straight line — confirming mathematical reasoning through visual feedback. This builds intrinsic motivation and readiness for more advanced algebra.

Error Opportunities & Misconceptions

Swapping axes (plotting days on y-axis and amount on x-axis).
Thinking “linear” just means a straight line without equal differences.
Choosing the wrong formula (d + 20 instead of 160 − 20d).
Misreading scales or miscounting 20 ml steps.

Transferability / Real-World Anchoring

Excellent. Linear change models appear in countless situations — fuel usage, savings decline, medicine dosage, or temperature change. Learners understand that consistent increase or decrease can be expressed and predicted mathematically.

Conceptual vs Procedural Balance

Strongly conceptual with procedural reinforcement. Students perform plotting and substitution steps (procedure) while developing insight into rate of change and linear structure — bridging arithmetic sequences and algebraic graphs.

Learning Objectives Addressed

Plot and interpret data on coordinate axes.
Recognise a linear decreasing pattern and describe its rate.
Write and evaluate the rule (Amount = 160 − 20d).
Explain why the pattern forms a straight line with constant differences.

What Your Score Says About You

Less than 20: You can read tables but struggle to link them to graphs — recheck axis placement and data plotting.
21–29: You follow the rule but may mix up coordinates or formulas — practise matching points to expressions.
31–39: You clearly understand the linear relationship — confident in table, graph, and algebra connections.
40 / 40: Mastery — you can generalise linear patterns and express them symbolically and graphically in any context.