Pythagoras’ Theorem 4A
Overview
In this Phlow, learners apply Pythagoras’ Theorem (a² + b² = c²) to find the hypotenuse of a right-angled triangle. The activity unfolds through a carefully scaffolded series of micro-steps, showing each part of the reasoning process in sequence.
Learners begin with the formula, substitute side lengths (e.g. 4² + 2²), expand to 16 + 4 = 20, take the square root (√20), and round the result (4.47 → 4.5 m). Each question isolates one skill, ensuring the learner understands why each step happens before moving on.
The integrated visuals link each algebraic line directly to the triangle diagram, helping students connect geometry with algebra and visualise how side lengths relate mathematically.
Worked Example
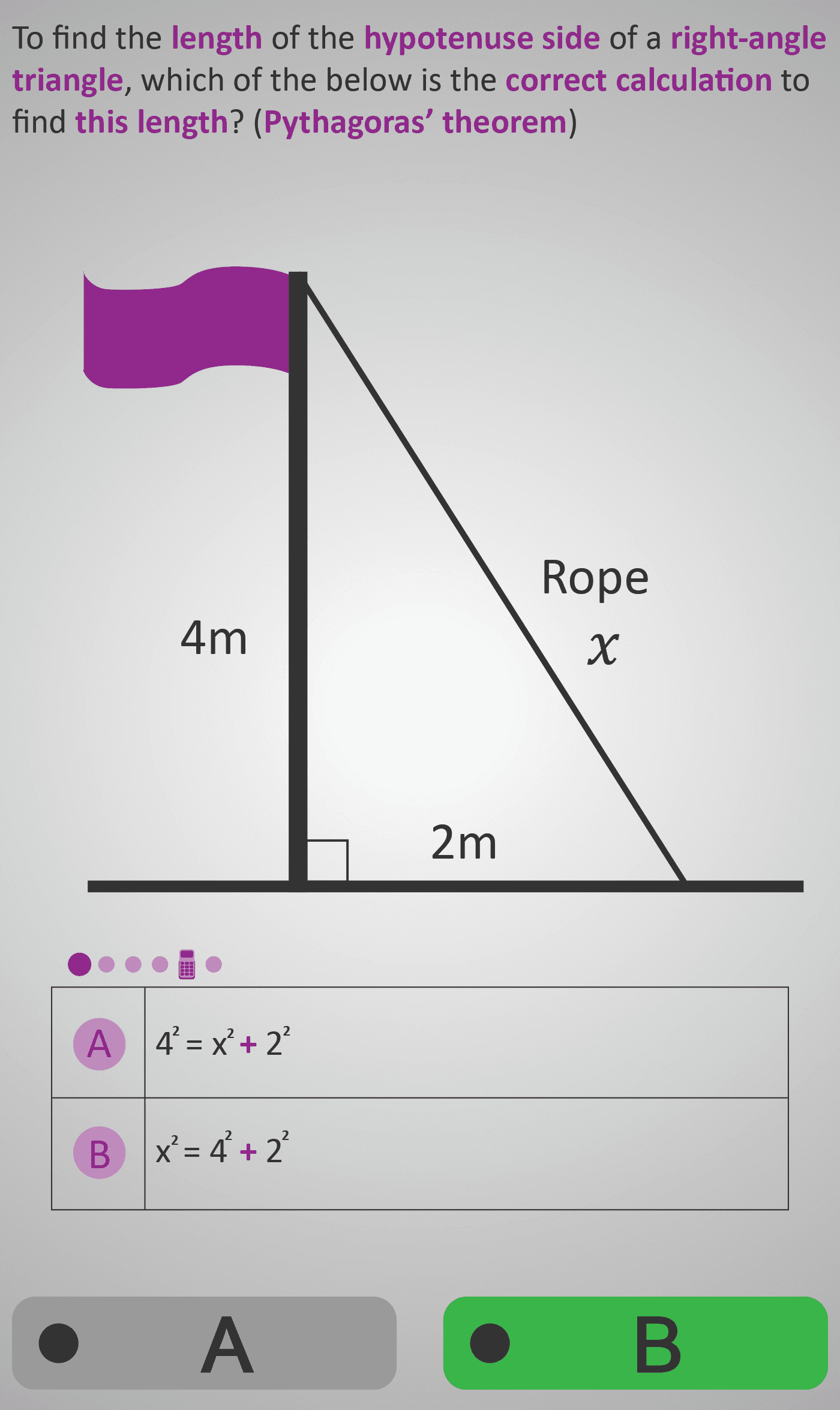
Given: Right-angled triangle with sides 4 m and 2 m.
Step 1: Formula → x² = 4² + 2²
Step 2: Expand → x² = 16 + 4
Step 3: Simplify → x² = 20
Step 4: Square root → x = √20 = 4.472...
Step 5: Round → x = 4.5 m
Sample Prompts
- Which side is the hypotenuse?
- Substitute the given lengths into the formula.
- What is the value of 4² + 2²?
- Round your final answer to one decimal place.
Why This Matters
This Phlow bridges geometry and algebra by connecting visual reasoning to symbolic calculation. Understanding Pythagoras’ Theorem is essential in engineering, architecture, navigation, and trigonometry. The guided progression from diagram to equation ensures conceptual clarity and procedural accuracy.
Prerequisite Knowledge Required
- Understanding of squared numbers (e.g., 4² = 16).
- Recognition of right-angled triangles and the hypotenuse.
- Familiarity with square roots and calculator use.
Linked Phlows:
Shapes 3B – Identifying Right Angles,
Squares & Roots 4A – Squaring and Square Roots,
Formula Substitution 4B – Substituting Values in Formulas.
Main Category
Geometry → Right-Angled Triangles and Measurement
Estimated Completion Time
Approx. 10–14 seconds per question.
40 questions total → Total time: 7–10 minutes.
| Learner Profile | Estimated Time | Description |
|---|---|---|
| One Level Below | 9–10 min | May need extra support with formula structure and calculator rounding. |
| At Level | 7–8 min | Applies the theorem fluently, checking each stage for accuracy. |
| One Level Above | 5–6 min | Completes calculations quickly and verifies results logically. |
Cognitive Load / Step Size
Excellent balance. Each screen introduces one concept only — formula recall, substitution, expansion, summing, square-rooting, or rounding. The small, predictable step size supports working memory while maintaining engagement.
Language & Literacy Demand
Moderate but well supported. Key mathematical terms (e.g. hypotenuse, square root, rounded) are highlighted in purple and paired with visuals. Concise instructions ensure that linguistic load never distracts from mathematical reasoning.
Clarity & Design
- Triangle diagrams visually aligned with formula steps.
- Purple highlights emphasise key symbols and results.
- Calculator icons signal when to compute or round.
- Clean white background focuses attention on the geometry and algebra link.
Curriculum Alignment (ROI Junior Cycle Mathematics)
- Strand: Geometry and Trigonometry
- Strand Unit: Right-Angled Triangles
- Learning Outcomes:
- Apply Pythagoras’ Theorem to find a missing side in a right-angled triangle.
- Relate square numbers and square roots to geometric length relationships.
- Round results to a specified degree of accuracy.
Engagement & Motivation
Real-world examples (e.g., flagpoles, ladders) make abstract geometry tangible. Each micro-step rewards success and maintains flow, helping learners feel capable and confident through steady progression.
Error Opportunities & Misconceptions
- Reversing the theorem (e.g., a² = b² + c²).
- Forgetting to square both sides before adding.
- Taking the square root prematurely.
- Rounding incorrectly (4.472 → 4.4 instead of 4.5).
- Misidentifying the hypotenuse as a shorter side.
Transferability / Real-World Anchoring
Highly transferable. Used in construction, navigation, architecture, and physics, Pythagoras’ Theorem bridges geometry and real-world problem-solving. It also prepares learners for trigonometric reasoning in later levels.
Conceptual vs Procedural Balance
Balanced and sequential. Learners build both procedural fluency (correctly executing the theorem) and conceptual understanding (why the formula works and what each term represents). Visuals and algebra are integrated to promote dual coding and deep comprehension.
Learning Objectives Addressed
- Identify the hypotenuse and apply Pythagoras’ Theorem accurately.
- Perform substitution, squaring, addition, and square-rooting steps with confidence.
- Round results correctly and interpret accuracy requirements.
- Connect geometric representation with algebraic notation.
What Your Score Says About You
- Less than 20: You may be unsure which side is the hypotenuse or when to apply square roots — revisit the early steps.
- 21–29: You understand the process but make small arithmetic or rounding errors — check each stage carefully.
- 31–39: You apply Pythagoras’ Theorem confidently and understand the reasoning — excellent progress.
- 40 / 40: Perfect mastery — you can explain each stage clearly and apply Pythagoras’ Theorem to any right-angled triangle.