Pythagoras’ Theorem 4B
Overview
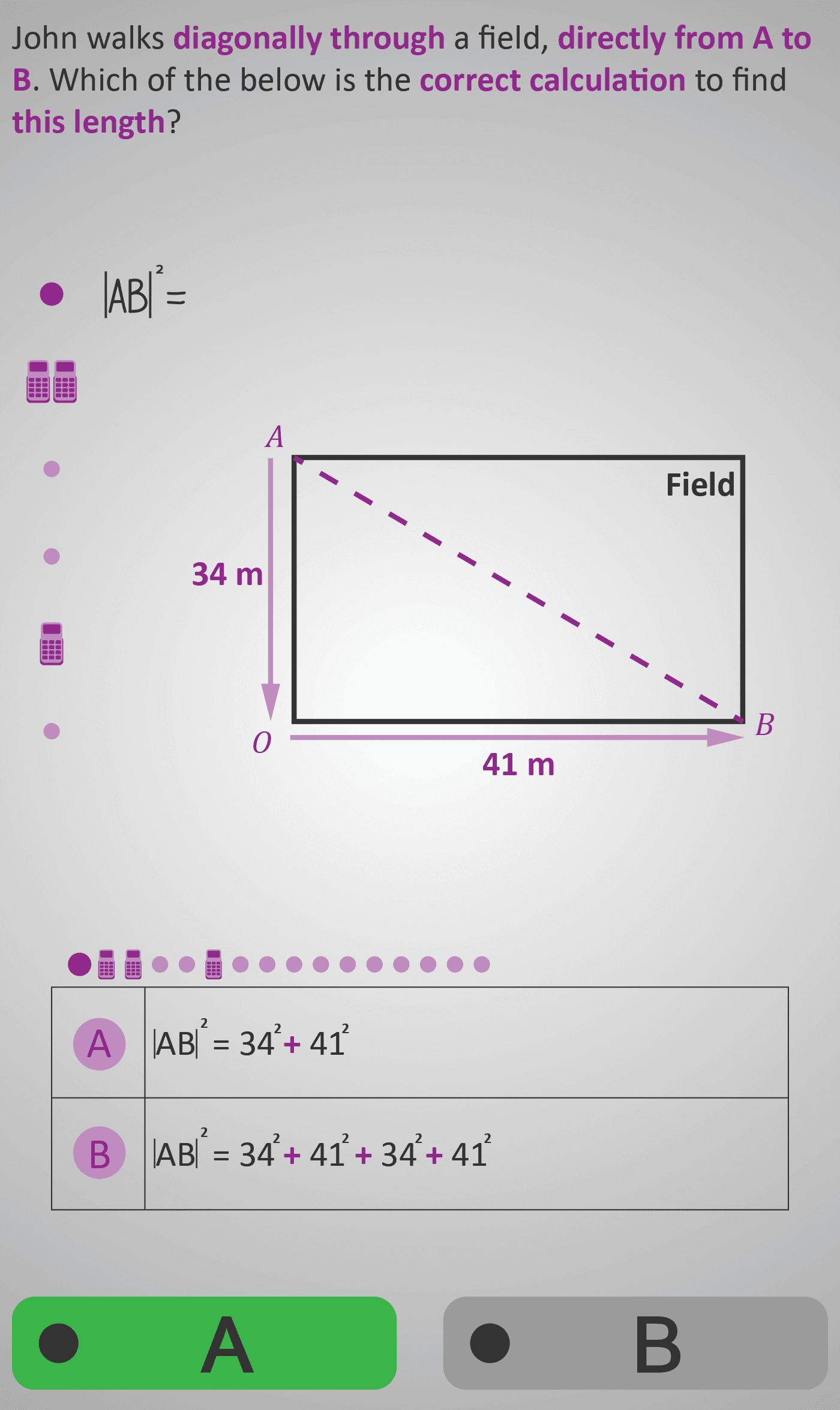
In this Phlow, learners apply Pythagoras’ Theorem to a real-world situation. John walks diagonally across a rectangular field from A to B, instead of around the edges. The field’s sides measure 34 m and 41 m.
Students calculate the diagonal length using the theorem: AB² = 34² + 41² → AB² = 1156 + 1681 = 2837. They then find AB = √2837 = 53.263... and round to one decimal place (53.3 m). Finally, learners compare this direct diagonal distance with the perimeter route (34 + 41 = 75 m) and calculate the difference: 75 – 53.3 = 21.7 m, approximately 22 m shorter.
The activity links geometric reasoning and numerical accuracy, encouraging students to interpret what their result means — not just compute it. It reinforces understanding of why Pythagoras’ Theorem matters in practical contexts.
Worked Example
Given: Sides = 34 m, 41 m
Step 1: Formula → AB² = 34² + 41²
Step 2: Square → AB² = 1156 + 1681
Step 3: Add → AB² = 2837
Step 4: Root → AB = √2837 = 53.263...
Step 5: Round → 53.3 m
Step 6: Compare → 75 – 53.3 = 21.7 m ≈ 22 m shorter
Sample Prompts
- Which formula helps find the diagonal of a right-angled field?
- What is 34² + 41²?
- Round your answer for the diagonal to one decimal place.
- How much shorter is the diagonal path compared with walking around?
Why This Matters
This Phlow transforms abstract algebraic calculation into real-world decision-making. Learners understand that geometry offers practical efficiency — the diagonal saves distance and time. It builds appreciation for how mathematics underpins spatial reasoning in everyday and professional contexts.
Prerequisite Knowledge Required
- Knowledge of Pythagoras’ Theorem (Phlow 4A).
- Calculator skills for squaring, square roots, and rounding.
- Basic addition and subtraction of decimal values.
- Understanding “difference” and “approximation to a given accuracy”.
Linked Phlows:
Squares & Roots 4A – Squaring and Square Roots,
Rounding 3C – Rounding Numbers to Specified Places,
Pythagoras 4A – Finding the Hypotenuse.
Main Category
Geometry → Measurement and Right-Angled Triangles
Estimated Completion Time
Approx. 12–15 seconds per question.
16 questions total → Total time: 7–9 minutes.
| Learner Profile | Estimated Time | Description |
|---|---|---|
| One Level Below | 9–10 min | May recheck rounding or subtraction; benefits from visual references. |
| At Level | 7–8 min | Applies the formula smoothly and interprets numerical comparisons correctly. |
| One Level Above | 5–6 min | Uses the calculator efficiently and explains geometric meaning confidently. |
Cognitive Load / Step Size
Excellent scaffolding. Each question introduces only one operation — squaring, adding, rooting, rounding, or comparing. The clear visuals and gradual reveal maintain flow, enabling focus on conceptual linkage (formula ↔ diagram ↔ difference).
Language & Literacy Demand
Moderate but supported. Key terms such as “difference”, “round”, and “nearest whole number” are colour-highlighted in purple. Visual aids — including the rectangular field, diagonal path, and calculator icon — ensure accessibility for EAL and lower-literacy learners.
Clarity & Design
- Field diagram clearly labels sides and diagonal (AB).
- Purple highlights draw attention to squaring, adding, and rounding steps.
- Clean layout integrates formula and visual reasoning seamlessly.
- Handwriting animation maintains rhythm and reinforces procedural fluency.
Curriculum Alignment (ROI Junior Cycle Mathematics)
- Strand: Geometry and Trigonometry
- Strand Unit: Right-Angled Triangles
- Learning Outcomes:
- Apply Pythagoras’ Theorem to practical real-life contexts.
- Perform calculations involving powers, roots, and rounding to a given accuracy.
- Interpret differences and compare distances meaningfully in context.
Engagement & Motivation
The relatable “field shortcut” context gives clear purpose to the mathematics — it answers “Why does this matter?” Learners feel the payoff of the theorem: the diagonal is shorter. The scenario encourages curiosity and satisfaction through real-world application.
Error Opportunities & Misconceptions
- Adding sides instead of squaring them (34 + 41).
- Taking √ of one term instead of the total.
- Incorrect rounding (53.263 → 53.2 instead of 53.3).
- Confusing subtraction and addition when finding the difference.
- Using approximate instead of exact values in final steps.
Transferability / Real-World Anchoring
Very strong. Understanding diagonal distances supports problem-solving in surveying, architecture, navigation, construction, and even sports. Students see how geometric reasoning saves effort in real life — the shortest distance is the diagonal.
Conceptual vs Procedural Balance
Perfectly balanced. The procedural skills (square, add, root, round) culminate in a conceptual insight — interpreting what the diagonal means and why it’s shorter. This connection transforms calculation into reasoning.
Learning Objectives Addressed
- Apply Pythagoras’ Theorem in a contextual problem.
- Use calculator functions accurately (powers, roots, rounding).
- Compare two distances and compute their difference.
- Interpret mathematical outcomes in real-world terms.
What Your Score Says About You
- Less than 10: You may still mix up formula order or rounding — revisit earlier steps for precision.
- 11–13: You can apply the formula but need to check your decimal accuracy and subtraction carefully.
- 14–15: You’re strong procedurally and conceptually — great progress!
- 16 / 16: Excellent mastery — you can explain why the diagonal is shorter and round perfectly to one decimal place.