Sin Cos Tan 4A
Overview
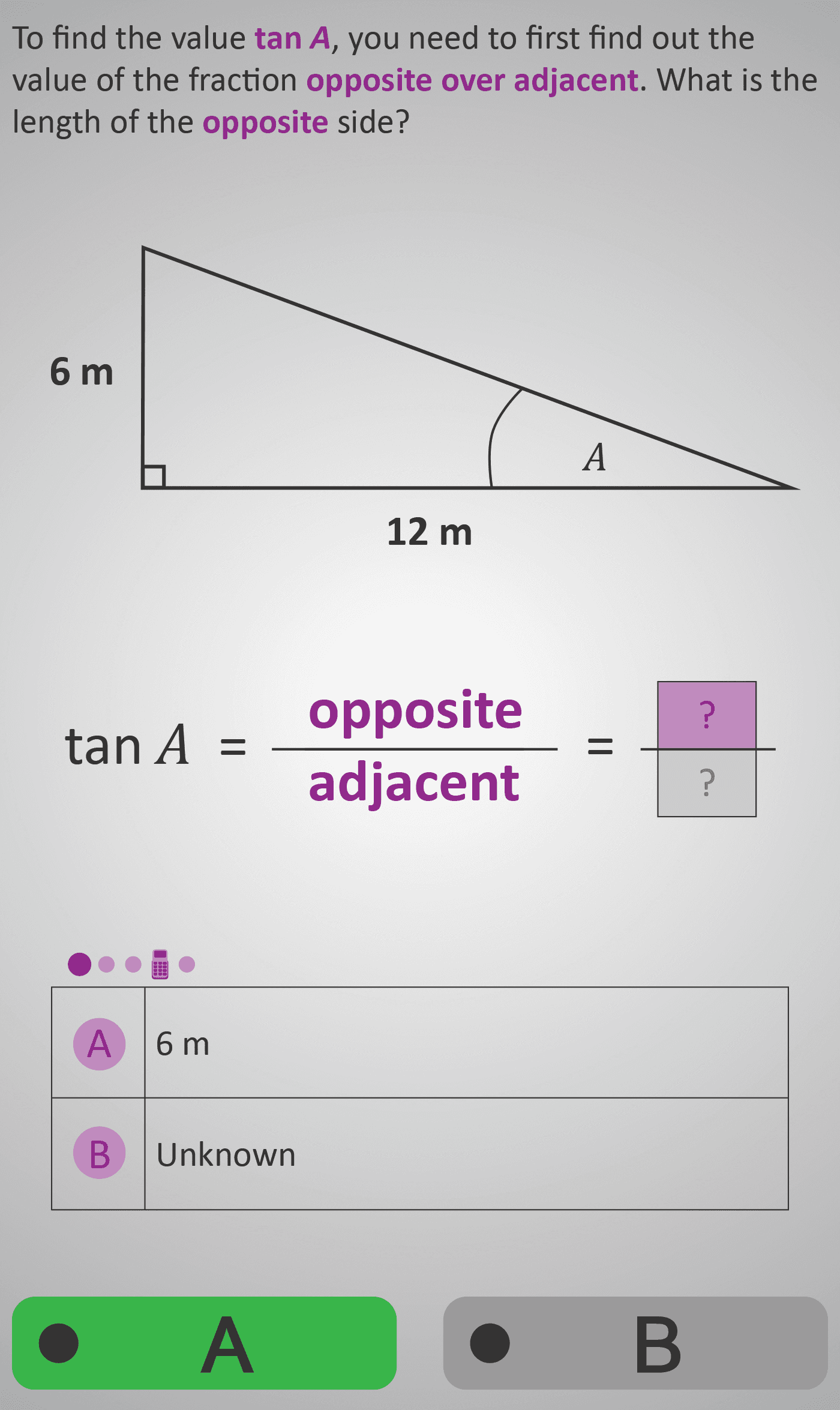
In this Phlow, learners discover how to work backwards from a trigonometric ratio to find an angle. Using a right-angled triangle labelled with 6 m (opposite) and 12 m (adjacent), students identify the correct sides, form the ratio tan A = opposite ÷ adjacent, and use their calculator’s tan⁻¹ key to find the missing angle.
Each screen introduces one small reasoning step — from identifying sides to forming the ratio and finally calculating and rounding the angle. This helps students connect the geometric meaning of tangent to its practical calculator application.
Worked Example
Given:
Opposite = 6 m
Adjacent = 12 m
tan A = 6 ÷ 12
tan A = 0.5
A = tan⁻¹(0.5)
A = 26.565° ≈ 27°
Step Sequence
- Identify the opposite and adjacent sides.
- Substitute into tan A = opposite ÷ adjacent.
- Press tan⁻¹ on the calculator and enter (6 ÷ 12).
- Round the result to the nearest degree.
Sample Prompts
- Which side is opposite angle A?
- What is the correct ratio for tan A?
- Which calculator key finds the angle?
- What is the angle rounded to the nearest degree?
Why This Matters
Understanding how to find an angle from side lengths is central to trigonometry. It connects geometric reasoning with calculator skills, preparing learners for real-world applications such as gradients, slopes, and navigation problems.
Prerequisite Knowledge Required
- Recognise right-angled triangles and angle notation.
- Understand sin, cos, and tan as ratios.
- Identify opposite, adjacent, and hypotenuse sides correctly.
- Use a calculator to enter brackets and perform divisions.
Linked Phlows:
Sin Cos Tan 3 – Introduction to Ratios,
Triangles 3 – Identifying Sides,
Ratios 3A–3C – Simplifying and Comparing Ratios.
Main Category
Geometry & Trigonometry
Estimated Completion Time
Approx. 10–14 seconds per question.
40 questions total → Total time: 7–10 minutes.
Cognitive Load / Step Size
Moderate and well-scaffolded. Each stage introduces a single idea: recognising sides, setting up the ratio, applying tan⁻¹, and rounding. Smooth transitions prevent overload and maintain flow.
Language & Literacy Demand
Low–medium. Key terms such as opposite, adjacent, and tan⁻¹ are colour-coded and paired with visuals. Sentences are concise, and instructions are supported by diagrams.
Clarity & Design
- Triangle diagram clearly labels sides relative to angle A.
- Consistent colour coding links text and visuals (purple = focus side).
- Calculator graphic shows correct tan⁻¹ key sequence.
- Step-by-step animation maintains clarity and pacing.
Curriculum Alignment (ROI Junior Cycle Mathematics)
- Strand: Measurement and Geometry
- Learning Outcomes: Apply trigonometric ratios to find unknown sides and angles; select appropriate formulae and use calculators effectively; round and interpret results to given accuracy.
Engagement & Motivation
The scenario feels practical and connected to real geometry problems. Step-by-step discovery and calculator interactivity sustain curiosity while reinforcing accurate reasoning.
Error Opportunities & Misconceptions
- Using tan instead of tan⁻¹ to find the angle.
- Swapping opposite and adjacent sides.
- Calculator in radians instead of degrees.
- Premature rounding or entry errors.
Transferability / Real-World Anchoring
Strong. These skills apply directly to slope calculations, construction, mapping, and navigation — wherever angles and distances meet in practice.
Conceptual vs Procedural Balance
Balanced. Learners both understand why the inverse tangent finds the angle and practise how to use it accurately.
Learning Objectives Addressed
- Identify opposite and adjacent sides in a right-angled triangle.
- Apply the tangent ratio to relate sides and angles.
- Use tan⁻¹ to calculate an unknown angle.
- Round results to an appropriate degree of accuracy.
What Your Score Says About You
- Less than 20: You may still mix up sides or use tan instead of tan⁻¹.
- 21–29: You understand the tan ratio but need more practice using the calculator and rounding.
- 31–39: You calculate accurately with minor input or rounding slips.
- 40 / 40: Excellent — you can confidently apply tangent to find any missing angle.