Sin Cos Tan 4B

Overview

This Phlow teaches students how to calculate the sine ratio for a given angle in a right-angled triangle. Using a triangle with a hypotenuse of 12 m and an opposite side labelled x, learners recall that sin θ = opposite ÷ hypotenuse and apply it to find sin(51°) with a calculator.

Each question builds in clear micro-steps: identifying the correct sides, forming the fraction, calculating sin(51°), and rounding the result to two decimal places. The process reveals both what sine means and how to find it accurately using digital tools.

Worked Example

Given:
θ = 51°
Opposite = x
Hypotenuse = 12 m

sin θ = opposite ÷ hypotenuse
sin(51°) = x ÷ 12

Calculator:
sin(51°) = 0.77714596…
≈ 0.78

Step Sequence

Identify the opposite and hypotenuse sides relative to θ.
Substitute into sin θ = opposite ÷ hypotenuse.
Use the calculator to find sin(51°).
Round the result to two decimal places.

Sample Prompts

Which side is the hypotenuse?
Which is the opposite side?
What fraction represents sin θ?
What is sin(51°) rounded to two decimal places?

Why This Matters

The sine ratio links angles directly to side lengths — a core idea in trigonometry. Learning how to calculate sin(θ) builds fluency for later problem-solving in geometry, physics, and real-world measurements.

Step 1 / 4

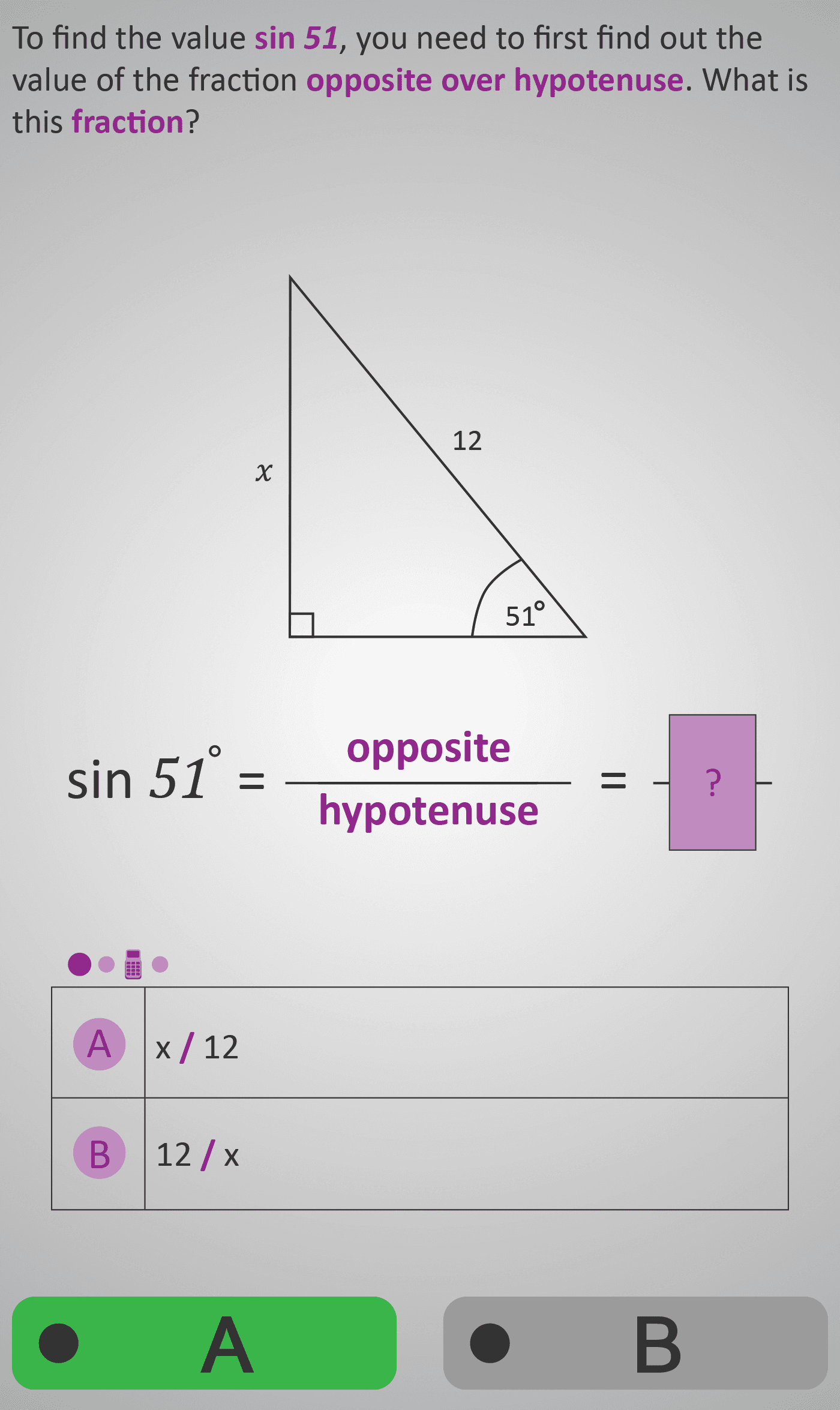
Prerequisite Knowledge Required

Recognise opposite and hypotenuse sides in right-angled triangles.
Understand that sin, cos, and tan relate angles to side ratios.
Use a calculator for trigonometric functions and rounding.
Know that angles are measured in degrees.

Linked Phlows:
Sin Cos Tan 4A – Finding an Angle Using Tangent, Triangles 3 – Recognising Sides, Ratios 3B–3C – Understanding Proportion.

Main Category

Geometry & Trigonometry

Estimated Completion Time

Approx. 10–14 seconds per question.
40 questions total → Total time: 7–10 minutes.

Cognitive Load / Step Size

Moderate and consistent. Each step introduces one focused action — identify, substitute, calculate, or round — maintaining clarity and supporting steady skill development.

Language & Literacy Demand

Low–medium. Mathematical terms (sine, opposite, hypotenuse, degree) are colour-coded and paired with visuals. The text is short, direct, and supported by clear numerical examples.

Clarity & Design

Large, labelled triangle highlights key sides and angles.
Purple ratio fraction mirrors the sin formula.
Calculator graphic models correct input syntax for sin(θ).
Sequential highlighting reinforces reasoning at each step.

Curriculum Alignment (ROI Junior Cycle Mathematics)

Strand: Geometry & Trigonometry
Learning Outcomes: Apply trigonometric ratios to find unknown sides and angles; use calculators for trigonometric evaluations; round results accurately to specified decimal places.

Engagement & Motivation

Seeing trigonometric ratios appear on-screen through calculator interaction provides a strong sense of discovery and understanding. The realistic visual cues (triangles, measurements) make it tangible and motivating.

Error Opportunities & Misconceptions

Reversing the ratio (12/x instead of x/12).
Entering sin(51) incorrectly or omitting degree mode.
Rounding errors (0.77 vs 0.78).
Confusing sine with division (thinking sin(51) = 51 ÷ 12).

Transferability / Real-World Anchoring

Highly transferable. This understanding supports applications in navigation, architecture, design, and surveying — wherever measuring angles or slopes is needed.

Conceptual vs Procedural Balance

Strong balance. Learners understand that sine represents a ratio (conceptual) and practise calculating it accurately (procedural). Recognising why sin(θ) is less than 1 deepens comprehension.

Learning Objectives Addressed

Identify opposite and hypotenuse sides in right-angled triangles.
Form the sine ratio correctly as sin θ = opposite ÷ hypotenuse.
Use a calculator to evaluate sin(θ).
Round to appropriate decimal places accurately.

What Your Score Says About You

Less than 20: You may confuse sides or calculator input.
21–29: You understand the concept but need more rounding and accuracy practice.
31–39: You apply sine confidently and calculate precisely.
40 / 40: Excellent — you’ve mastered evaluating sine values and interpreting them correctly.